17.15. Дифференциальные операции 1го порядка

1°. Для векторного поля Ai образуем градиент векторного поля , а затем получившийся тензор свернем по индексам I, J : .

Как известно, такая величина в векторном анализе называется дивергенцией векторного поля А ( divA ). Подобным образом можно получить дивергенцию тензорного поля любого ранга, выше нулевого.

Результирующее тензорное поле имеет ранг на единицу меньший, чем исходное поле.

Для тензорного поля ранга R можно получить R различных тензорных полей (R – 1)го ранга типа «дивергенции» в зависимости от того, какой из индексов исходного поля сворачивается с индексом дифференцирования: .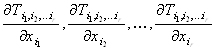

2°. В векторном анализе известна такая дифференциальная операция, как rotA = Ñ´A. В тензорном представлении . Оператором можно действовать на тензор любого ранга выше нулевого и затем сворачивать индекс L с одним из индексов этого тензора. Результирующее тензорное поле имеет тот же ранг, что и исходное.

Для тензорного поля ранга R можно получить R различных тензорных полей RГо ранга типа «ротор» в зависимости от того с каким из индексов исходного поля сворачивать индекс L.

.

3°. Схематически операции градиента, дивергенции и ротора тензорного поля произвольного ранга можно задать следующим образом:

(gradT…)I = ,

(divT…I…) = ,

(rotT…L…) = .

< Предыдущая		Следующая >