17.16. Дифференциальные операции 2го порядка

1°. Для скалярной функции φ: 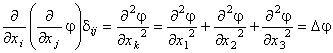, и такая величина называется лапласианом функции.

Аналогично можно ввести лапласиан произвольного тензора ранга R и получить тензорное поле того же ранга: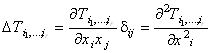

Рассмотрим divrotA, где А – произвольное векторное поле:

Div rotA =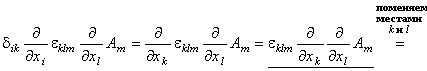

.

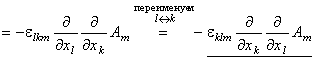Равенство подчеркнутых выражений позволяет заключить, что divrotA = 0 для любого векторного поля А.

Аналогичное тождество имеет место для тензорного поля любого ранга (кроме нулевого): .

3°. Проверим справедливость тождества: rot rot = grad div - Δ.

◀ (rot rot A)I =

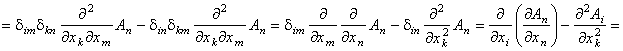
(divA) - (DA)I = (grad divA)I - (DA)I = (grad divA - DA)I ▶

Аналогичное тождество можно записать и для произвольного тензорного поля.

< Предыдущая		Следующая >