17.02. Взаимные базисы. Ковариантные и контравариантные координаты векторов

Пусть EN – евклидово пространство, пусть {E1, E2, …, EN } Базис в EN И {E1, E2, …, EN} Другой базис в EN. Базисы {Ei}И {Ei} называются взаимными, если (Ei, Ej) = = .

­символ

Кронекера-Капелли.

Т°. Любой базис {EI} из En имеет единственный взаимный базис.

◀ Пусть Ej = E1 + E2 + … +En. Умножим равенство скалярно на EI.

(Ei, Ej) = (Ei, E1) + (Ei, E2) + … + (Ei, En) = , I, J = 1, 2, …, N.

Имеем неоднородную систему N-линейных уравнений с N неизвестными , Определитель этой системы есть Г(E1, E2, …, EN) ¹ 0, т. е. система имеет единственное ненулевое решение.

Следовательно векторы Ej определяются однозначно. Убедимся в том, что они образуют базис (т. е. являются линейно независимыми).

Пусть a1E1 + a1E2 + …+ aNEn = 0. Умножим скалярно на EI.

A1(Ei, E1) + a2(Ei, E2) + … + aN(Ei, En) = 0 Þ aI = 0, I, J = 1, 2, …, N ▶

Замечание: если базис {Ei} ортонормированный, то его взаимный базис совпадает с данным базисом.

Пусть {Ei} и {Ej} взаимные базисы в ЕN.

Тогда "хÎЕN (1)

(X1, X2, …, XN) Называются ковариантными координатами вектора X.

(X1, X2, …, XN) Называются контравариантными координатами вектора X.

Смысл названий мы поясним далее.

Соглашение: Пусть имеется выражение, составленное из сомножителей, которые снабжены конечным числом индексов (верхних и нижних). При этом договариваются, что все нижние индексы обозначаются разными символами (аналогично верхние). Если в таком выражении встречаются два одинаковых индекса, из которых один верхний, а другой – нижний, то считается, что по таким индексам производится суммирование от 1 до N.

Например: .

Используя, это соглашение формула (1) записывается так: X = Xiei, X = Xiei, (индекс суммирования может быть обозначен любым символом, результат не изменится – и часто Называется «немым» (иногда «глухим») индексом).

Пусть X = Xiei. Умножив на Ej, получим (X,Ej) = Xi(Ei,Ej) = Xi = Xj. Аналогично X = Xiei умножим на Ej и получим (X,EJ) = Xi(Ei,Ej) = Xi = Xj. Т. е. получили формулы:

Эти формулы Называются формулами Гиббса.

Тогда используя формулы Гиббса, запишем: Ej = (Ej,Ei)Ei и Ej = (Ej,Ei)Ei И обозначив Gji = (Ej,Ei) , Gji = (Ej,Ei) получим Ej = Gjiei; Ej = Gjiei.

 

Т. е. для получения взаимного базиса {Ej} по базису {Ei} достаточно знать матрицу Gji = (Ej,Ei) и наоборот: для получения базиса {Ej} По базису {Ei} достаточно знать матрицу Gji = (Ej,Ei) . (Точнее их обратные матрицы).

Т°. Матрицы Gji и Gji – Взаимнообратные.

◀ Соотношение Ei = Gjiej умножим на Ek : = (Ei,Ek) = Gji(Ej,Ek) = Gjigjk Þ Gjigjk = , т. е. произведение матриц (Gji) и (Gji) есть единичная матрица ▶

Задача 1. По заданному базису {Ei} (нижнему) построить ему взаимный базис {Ei} (верхний), по заданному верхнему базису построить взаимный нижний.

◀ а) Чтобы построить базис взаимный к нижнему надо найти матрицу GH = (Gik) = (Ei, Ek), обратить матрицу, получив (GH)–1 и подействовать этой матрицей на матрицу FH, строками которой являются векторы нижнего базиса. После перемножения получится матрица FB, строками которой являются векторы верхнего базиса.

б) Чтобы построить базис взаимный к верхнему надо найти матрицу GВ = (Gik) = (Ei, Ek), обратить ее, получив (GВ)–1 и подействовать этой матрицей на матрицу FB, строками которой являются векторы верхнего базиса. После перемножения получится матрица FH,

Строками которой, являются векторы нижнего базиса.

В) именно так трактуются формулы: Ei = Gijei = (Gij)–1Ei; Ei = Gijei = (Gij)–1Ei ▶

Примеры.

1°. Найти базис, взаимный к базису: Е1(1, 1, 0), Е2(1, 0, 1), Е3(0, 1, 1).

◀ а) Строим матрицу: 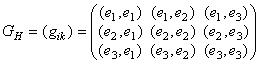. Получаем: ;

.

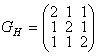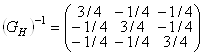Б) Составляем матрицу ;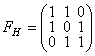

В) и находим: .

Г) Строки полученной матрицы FB и есть векторы взаимного базиса, т. е.

Е1(1/2, 1/2, –1/2), Е2(1/2, –1/2, 1/2), Е3(–1/2, 1/2, 1/2) ▶

2°. Найдем базис взаимный к базису: Е1(1, 1, 1), Е2(0, 1, 1), Е3(0, 0, 1).

◀ Строим матрицу: 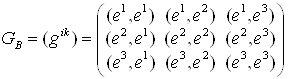, т. е. 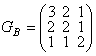; 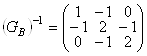. Находим .

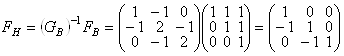Таким образом найдены векторы взаимного базиса: Е1(1, 0, 0), Е2(–1, 1, 0), Е3(0, –1, 1) ▶

Задача 2. Вектор Х (5, 2, 1) задан своими координатами в том же базисе, в котором заданы векторы двух взаимных базисов: Е1(1, 1, 0), Е2(1, 0, 1), Е3(0, 1, 1) и Е1(1/2, 1/2, –1/2), Е2(1/2, –1/2, 1/2), Е3(–1/2, 1/2, 1/2). Найти ковариантные и контравариантные координаты вектора Х в базисе {E1, E2, E3, E1, E2, E3}.

◀ Вектор X = (Xei)Ei = 7E1 + 6E2 + 3E3 поэтому (Х1, Х2, Х3) = (7, 6, 3) – ковариантные координаты Х.

Вектор X = (Xei)Ei = 3E1 + 2E2 – E3, следовательно (Х1, Х2, Х3) = (3, 2, –1) – контравариантные координаты Х ▶

< Предыдущая		Следующая >