17.01. Элементы теории тензоров. Определитель Грамма

Def: Определителем Грамма, системы векторов {E1, E2, …, EK} Называется определитель

Г(E1, E2, …, EK) = .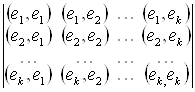

Т°. Для того чтобы система векторов {E1, E2, …, EK} евклидова пространства EN была

линейно-зависимой необходимо и достаточно чтобы Г(E1, E2, …, EK) был равен

нулю.

◀ Необходимость. Пусть E1, E2, …, EK Линейно зависимы. Тогда EK = a1E1 + a2E2 +…+ EK–1aK–1 и в Г(E1, E2, …, EK) элементы последней строки имеют вид a1(E1,EI) + a2(E2,EI) + …+ aK–1(EK–1,EI), т. е. последняя строка есть линейная комбинация остальных Þ Г(E1, E2, …, EK) = 0.

Достаточность. Пусть Г(E1, E2, …, EK) = 0 Þ строки его линейно зависимы Þ $b1, b2, …, bK b1(E1,EI) + … + bK(EK, eI) = 0 Þ (b1E1 + … + bKeK = 0 и не все bI = 0 Þ E1, E2, …, EK Линейно зависимы. Противоречие ▶

Следствие. Если E1, E2, …, EK Линейно независимы, то Г(E1, E2, …, EK) ¹ 0. Более того, Г(E1, E2, …, EK) > 0

◀ Рассматриваем ℒ(E1, E2, …, EK). Тогда (EK, eI) – элементы матрицы некоторой симметрической билинейной формы, соответствующая которой квадратичная форма определяет скалярное произведение, т. е. является положительно определенной. Следовательно, по критерию Сильвестра D1 > 0, D2 > 0, …, DK > 0. Но DK = Г(E1, E2, …, EK) ▶

< Предыдущая		Следующая >