16.14. Приводимые и неприводимые представления

Def: Подпространство Е¢ называется инвариантным для представления D(G), если оно инвариантно для всякого оператора из D(G).

Очевидно, что на инвариантном подпространстве Е¢ представления D(G) индуцируется некоторое представление , которое, вообще говоря, не сводится к D(G) если Е¢ ¹ Еn.

Представление Называется частью представления D(G).

Поясним теперь понятие представления.

Пусть, например, все матрицы некоторого трехмерного представления D(G) имеют вид 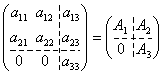. Нетрудно проверить, что при умножении матриц такого типа их структура сохраняется, причем и (т. е. части А1 и А3 перемножаются автономно).

Отсюда следует, что А1 есть двумерное представление группы G, а А3 есть одномерное представление этой же группы.

В таких случаях говорят, что представление D(G) Приводимо.

Если все матрицы (речь идет о квадратных матрицах ) имеют вид 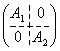, где А1 и А2 квадратные матрицы порядков N1 и N2 , то матрицы А1 и А2 образуют представления, сумма размерностей которых N1 + N2 = N.

В этом случае представление Называют Вполне приводимым.

И в заключение: Представления D(G) называется неприводимым, если у этого представления существуют лишь два инвариантных подпространства: Еn и {θ}.

Роль неприводимых представлений заключается в том, что любое представление может быть выражено через неприводимые.

< Предыдущая		Следующая >