16.12. Группа Лоренца

В физике, при изучении поведения тел (частиц) в пространстве и времени, часто полезно, из наглядных соображений, пользоваться 4х-мерным пространством векторов с координатами (Ct, X, Y, Z)) (C – скорость света)). Такое пространство называется мировым пространством.

В этом пространстве событие изображается точкой в мировом пространстве или мировой точкой.

Частице в мировом пространстве соответствует мировая линия.

Пусть в некоторой инерциальной системе отсчета К из точки (X1, Y1, Z1) в некоторый момент времени T1 отправлен сигнал со скоростью С и этот сигнал принят в точке (X2, Y2, Z2) в момент времени T2. Тогда расстояние, которое этот сигнал прошел, равно: , следовательно: C2(T2 - T1)2 - (X2 - X1)2 - - (Y2 - Y1)2 - (Z2 - Z1)2 = 0. В другой инерциальной системе отсчета К¢ будем иметь:

C2(T¢2 - T¢1)2 - (X¢2 - X¢1)2 - (Y¢2 - Y¢1)2 - (Z¢2 - Z¢1)2 = 0.

Принцип неизменности скорости света в различных системах отсчета в математической интерпретации обозначает, что не изменяется величина S, где: S2 = C2(T2 - T1)2 - (X2 - - X1)2 - (Y2 - Y1)2 - (Z2 - Z1)2 .

Величина S Называется интервалом между двумя событиями в мировом пространстве.

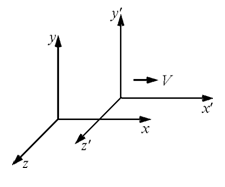Преобразования, описывающие переход от одной инерциальной системы отсчета К к другой инерциальной системе отсчета К¢, движущейся относительно К с постоянной скоростью V в предположении бесконечности скорости света Называются преобразованиями Галилея:

(X¢ = X +Vt, Y¢ = Y, Z¢ = Z, T¢ = T).

Если же учитывать конечность скорости света, то такие преобразования носят Названия преобразований Лоренца. Преобразования Лоренца сохраняют интервал. Если в указанном пространстве ввести: , то все векторы (и интервалы) разобьются на:

А) времени-подобные (s(X) > 0);

Б) изотропные (s(X) = 0);

В) пространственно-подобные (s(X) < 0).

Если интервал между событиями времени-подобен, то существует К¢ в которой два события произошли в одном и том же месте мирового пространства.

Если интервал между событиями пространственно-подобен, то существует К¢ в котором два события произошли одновременно.

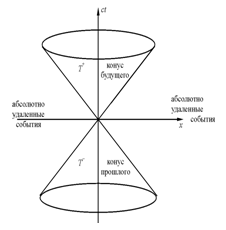Два события могут быть связаны причинно-следственной связью, если интервал между ними времени-подобный.

Рассмотрим псевдоевклидово пространство Еn(P, Q) в котором скалярное произведение (X, Y) задано симметричной невырожденной билинейной формой, полярной знакопеременной квадратичной форме A(X, X), которая в некоторой системе координат(она называется Галилеевой) имеет вид: .

Def: Линейное преобразование Р псевдоевклидового пространства Еn(P, Q) называется преобразованием Лоренца, если "X, YÎEn(P, Q), (Рx, Рy) = (X, Y).

Тº. Определитель преобразования Лоренца отличен от нуля и, следовательно, существует P-1. Доказать самостоятельно.

Тº. Произведение преобразований Лоренца есть преобразование Лоренца. Доказать

самостоятельно.

Таким образом:

Тº. Множество всех преобразований Лоренца псевдоевклидового пространства

Еn(P, Q) c обычной операцией умножения линейных операторов образуют

группу, которая называется общей группой Лоренца псевдоевклидового

пространства Еn(P, Q) и обозначена L(N; P, Q). Доказать самостоятельно.

Группа L(N; 1, N-1) обозначается L(N). Группа Лоренцевых преобразований в рассмотренном выше Е4(1, 3) обозначается L(4).

Подгруппа группы L(N) преобразований Р, которые времени-подобные векторы переводят во времени-подобные векторы Называется полной группой Лоренца и обозначается L­(N).

Подгруппа группы L(N) преобразований Р, для которых detP > 0 Называется собственной группой Лоренца и обозначается L+(N).

Собственные преобразования Лоренца, которые принадлежат L(N) т. е. переводят времени-подобные векторы во времени-подобные векторы также образуют подгруппу L(N), которая называется группой Лоренца и обозначается L­(N).

< Предыдущая		Следующая >