16.01. Элементы теории групп. Понятие группы. Подгруппы

Множество G элементов X, Y, Z, … произвольной природы называется группой, если в нем корректно введена внутренняя операция (закон композиции) т. е. "Х, YÎG, $ZÎG такое, что Z = X⊕Y или (Z = X⊙Y), удовлетворяющее условиям:

1) X⊕(Y⊕Z) = (X⊕Y)⊕Z ассоциативность 1) X⊙(Y⊙Z) = (X⊙Y)⊙Z;

2) $qÎG½"XÎG X⊕q = X нейтральный элемент 2) $ЕÎG½"XÎG X⊙Е = X;

3) обратный элемент 3) .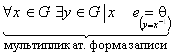

Если введенная операция еще и коммутативная, т. е. X⊕Y = Y⊕X Или (X⊙Y = y⊙X), то группа Называется абелевой.

Подмножество элементов G1 группы G Называется подгруппой, если:

1) "Х, УÎG1 ® X⊙YÎG1; 2) "ХÎG1 ® X-1ÎG1.

(Здесь применена мультипликативная форма записи)

Подгруппа G1 группы G сама по себе является группой. Простейшими (тривиальными) подгруппами любой группы является сама группа и группа, состоящая из одного элемента – нейтрального.

< Предыдущая		Следующая >