13.2. Примеры приведения матриц к жордановой форме

1°. 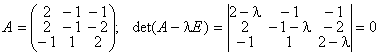. Корни характеристического уравнения: l1, 2, 3 = 1. .

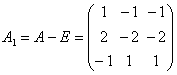Собственные векторы А по λ = 1, т. е. ядро А1:

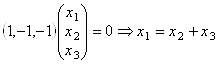, значит базис N(А1): .

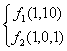Образ оператора А1 М(А1) находим из соотношений:

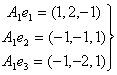; базис М(А1) F3(1, 2, –1), и т. к. F3 = 2F1 – F2, то F3Îℒ(F1, F2).

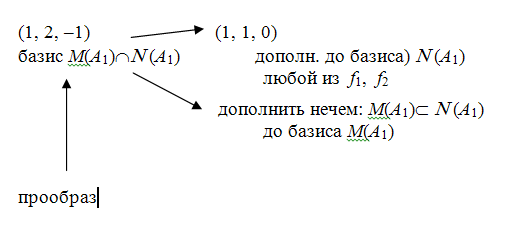
А1У = (1, 2, –1) Þ У1 – У2 – У3 = 1 , например (1, 0, 0)

Кстати: А1У = (1, 0, 0), такого У не существует, т. е. прообраза второго слоя для (1, 2, –1) нет.

Жорданов базис оператора А: 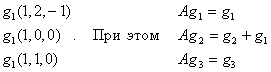. И, окончательно, имеем жорданову форму матрицы оператора А: .

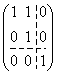2°. ; det(A - lE) = 0 l1, 2 = 1; l3, 4 = 2.

A) Рассмотрим оператор А1: А1-E=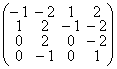. Ищем собственные векторы оператора А при l = 1, т. е. ядро оператора А1.

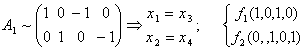. Векторы {F1,F2} образуют базис N(A1).

Далее ищем базис.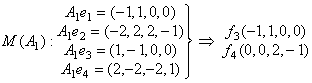

Так как векторы F1, F2, F3, F4 – линейно независимы, то:

(1, 0, 1, 0), (0, 1, 0, 1)

………………. уже 2 вектора.

нет векторов (–1, 1, 0, 0), (0, 0, 2, –1)

Кратность корня λ = 1 равна двум, поэтому имеем два вектора жорданового базиса А:

G1(1, 0, 1, 0); G2(0, 1, 0, 1).

Б)Рассмотрим оператор А2=А-2Е: 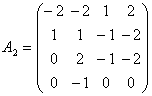, и найдем ядро оператора А2 т. е. собственные вектора А при λ = 2. 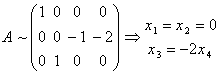. { F1(0, 0, –2, 1)}

базис ядра

Ищем базис образа оператора А2 – М(А2) .

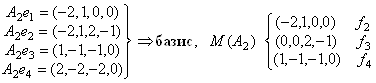
М(А2)ÇN(A2) = ℒ(0, 0, 2, –1).

Тогда, согласно схеме: ………………………

(0, 0, –2, 1)

(–2, 1, 0, 0), (1, –1, –1, 0)

А2У = (0, 0, –2, 1).

Решаем систему А2У = (0, 0, –2, 1), для нахождения прообраза 1-го слоя вектора (0, 0, –2, 1) Получаем: .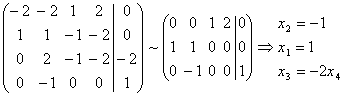

Решением системы является, например, вектор (1, –1, 0, 0).

Тогда G3(0, 0, –2, 1); G4(1, ­1, 0, 0).

Для оператора А найден жорданов базис: .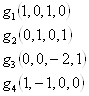

При этом 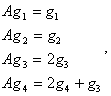т. е. жорданова форма оператора А: .

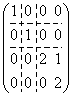< Предыдущая		Следующая >