10.5. Спектральное разложение эрмитового оператора. Теорема Гамильтона – Кэли

Пусть А – эрмитов оператор; l1 ³ l2 ³ … ³ lN собственные значения этого оператора и {Е1, Е2, …, Еm} – соответствующий им ортонормированный собственный базис. Тогда "XÎV ; Ax = .

Def: Оператор Рk: Pkx = (X, ek)Ek, называется оператором-проектором или просто проектором на одномерное пространство, порожденное вектором {Ek}.

Свойства проекторов:

1°. Pk – самосопряженный (эрмитов).

◀ (Pkx, Y) = ((X, ek)Ek, Y) = (X, ek)(Ek, y) = (X, ek) = (X, (Y, ek)Ek) = (X, Pky) ▶

2°. = Pk. ◀ = Pk(Pkx) = Pk(X, ek)Ek = (X, ek)Pek = (X, ek)(Ek, ek)Ek = (X, ek)Ek = Pkx ▶

3°. PkPj = 0, (X ¹ J). ◀ PkPj x = Pk(Pj x) = Pk(X, ej)Ej = (X, ej)Pkej = (X, ej)Ek = 0 ▶

Для операторов-Проекторов Pk Имеем:

.

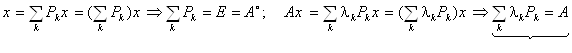Такое представление эрмитового оператора А называется его спектральным разложением. Обратим еще внимание: .

Def: Пусть Р(λ) – произвольный полином РЙ – степени, т. е. . Тогда определим полином от оператора слеующим образом: .

Тº. (Гамильтона-Кэли). Эрмитов оператор А является корнем своего

характеристического полинома: если .

◀ ▶

< Предыдущая		Следующая >