10.4. Еще о свойствах эрмитового оператора

Т°. Чтобы линейный оператор АÎL(V, V) был эрмитов необходимо и достаточно,

чтобы Im(Ax, X) = 0.

◀ Прежде всего, отметим, что "АÎL(V, V) $AR, AIÎL(V, V) такие что A = AR +IAI и, кроме того АR И АI – эрмитовы. Следовательно, (ARx, x)ÎR и (AIx, x)ÎR, т. е. (Ax, x) = =.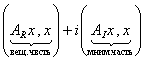

Теперь:

Необходимость. Пусть А = А* Þ (Ах, Х)ÎR Þ Im(Ах, Х) = 0.

Достаточность. Пусть Im(Ах, Х) = 0 Þ (AIx, x) = 0 Þ Þ ||AI|| = 0 Þ AI = 0 Þ

Þ A = AR Þ AR – эрмитов ▶

Т°. Если А – эрмитов оператор и λ – его собственное значение, то $ХÎV, ||Х|| = 1, и

l = (Ах, Х).

◀ Пусть Z - собственный вектор оператора А, соответствующий собственному значению λ:

Аz = λZ Þ 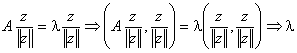= (Ах, Х),

Где Х – собственный вектор и ||Х|| = 1 ▶

Следствие: Пусть А – эрмитов оператор и M = . Тогда для собственных значений λ оператора А справедливо M £ l £ M.

Т°. Если А – самосопряженный (эрмитов) оператор и "XÎV; (Ax, X) ³ 0, то

||A|| = lmax

◀ . Обозначим l = (Ax0, X0) = ||A||. Рассмотрим

||(A – lЕ)Х0||2 = (Ax0 – lX0, Ax0 – lX0) = (Ax0, Ax0) – l(Х0, Ах0) – (Ax0, X0) + l(Х0, Х0) =

= = (Ax0, Ax0) – l(Ах0, Х0) – l(Ах0, Х0) + l2(Х0, Х0) = =

= ||Aх0||2 – 2||A||2 + ||A||2 = 0, т. е. ||(A – lЕ)Х0|| = 0 Þ (A – lЕ)Х0 = 0 Þ Aх0 = lХ0, т. е. l – собственное значение ▶

Продолжаем изучение спектральных свойств эрмитовых операторов.

Т°. Пусть для эрмитового оператора А M = ; тогда M и

М – наименьшее и наибольшее собственное значение оператора А.

◀ Достаточно доказать, что M и М – собственные значения оператора А.

1) Рассмотрим оператор B = A – ME Þ В – эрмитов Þ (Вх, Х) = (А(Х), Х) – M(Х, Х) ³ 0. Т. е. В – эрмитов, (Bx, X) ³ 0 Þ || B || = lmax, но , т. е. для В: lmax = M – M Þ $X0 Bx0 = (M – M)X0 Þ (A – ME)X0 = Mx0 – Mx0 Þ Ax0 – Mx0 = = Mx0 – Mx0 Þ Ax0 = Mx0 Þ Mx0 – собственное значение оператора А.

2) Рассмотрим В = –А Þ В – эрмитов. Þ Þ – M – собственное значение В

Þ $Х Вх = – M Þ –Ах = – Mх Þ Ах = Mх, т. е. M – собственные значения А ▶

Тº (о собственном базисе эрмитового оператора). Если А – эрмитов оператор: АÎL(V, V) в N-мерном унитарном пространстве, то в V существует N-линейно-независимых, попарно ортогональных и единичных собственных векторах.

◀ 1) А – эрмитов, АÎL(V, V) = lmax = l1 = и $Е1 – единичный собственный вектор с собственным значениям l1: Ае1 = l1Е1. Обозначим V1 = ℒ^(Е1). При этом V = V1 Å ℒ(Е1). Оказывается V1 – инвариантно относительно А. В самом деле

"ХÎV1: (Ах, е1) = (Х, Ае1) = l1(Х, Е1) 0, т. е. (Ах, е1) = 0 Þ .

2) Теперь можем рассмотреть А в V1: АÎL(V1, V1), А – эрмитов Þ lmax = l2 =

И $Е2 – единичный вектор, такой, что Ае2 = l2 Е2 и Е2 ^ Е1.

Рассмотрим V2 = ℒ^(Е1, Е2). Тогда V = V1 Å ℒ(Е1), V2 – инвариантно относительно А.

"ХÎV2: (Ах, a1Е1+a2Е2) = (Х, А(a1Е1) + А(a2Е2)) = 0,

Ах^a1Е1 +a2Е2 Þ "ХÎV2.

3) …

4) …

Итак, $E1, …, En - единичные, взаимно ортогональные и собственные векторы,

т. е. в V существует ортонормированный базис, состоящий из собственных векторов оператора А ▶

Примечание: Договоримся, в дальнейшем, нумеровать собственные значения в порядке их убывания с учетом кратности, т. е. l1 ³ l2 ³ … ³ lN и соответствующие им векторы Е1, Е2, …, Еn обладают свойством (Ei, Ej) = dIj.

Примечание: Из доказанной выше теоремы следует: 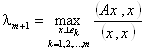, или , где Еm = ℒ(Е1, Е2, …, Еm).

Т° (минимаксное свойство собственных значений). Пусть А – эрмитов оператор и l1 ³ l2 ³ … ³ lN его собственные значения, тогда где ℇM –множество всех M-мерных подпространств пространства V.

Доказать cамостоятельно.

< Предыдущая		Следующая >