10.3. Норма оператора

Def: Нормой линейного оператора AÎL(V, V) называется число ||A|| определяемое равенством ||A|| = .

Из определения нормы линейного оператора возникает очевидное и очень полезное неравенство ||A|| £ ||A||×||Х|| .

Т°. Для эрмитового оператора А: ||A|| = .

◀ Обозначим m =.

1) Вспомним неравенство Коши-Буняковского (Х, У)2£ (Х, Х)(У, У) запишем |(Х,У)|£ ||X||×||Y|| Þ

Þ |(Aх, X)| £ ||Ax||×||X|| £ ||Ax||×||X||×||X|| = ||A||×||X||2, т. е. |(Aх, X)| £ ||A||×||X||2 и пусть ||X|| = 1.

|(Aх, X)| £ ||A||

Т. е. m £ ||A|| (*)

2) Отметим: |(Az, Z)| £ |(Az/||Z||, z/||Z||)| × ||Z||2 £ ||Z||2 × sup|(Az/||Z||, z/||Z||)|,

Т. е. |(Az, Z)| £ m||Z||2 и теперь рассмотрим разность:

(A(Х + У), Х + У) – (А(Х – У), Х – У) = (Ах, Х) + (Ах, У) + (Ау, Х) + (Ау, У) – (Ах, Х) + (Ах, У) + (Ау, Х) – (Ау, У) = 2(Ах, У) + 2(Ау, Х) = 2((Ах, У) + (У, Ах)) = 2((Ах, у) + ()) = 4Re(Ах, У), т. е. 4Re(Ах, У) = (A(X + Y), X + Y) – (А(Х – У), Х – У).

Тогда:

4|Re(Ах, У)| = |(A(X + Y), X + Y) – (А(Х – У), Х – У)| £ |(A(X + Y), X + Y)| + |(А(Х– У), Х– У)| £

£ m((X+ Y, X + Y) + (Х– У, Х– У)) = m((X, X) + (Y, Y)+ (Х, У)+ (Y, X) + (X, X) +(Y, Y) – (X, Y) – (Y, X)) =

= 2m((X, X) + (Y, Y)) = 2m (||X||2 + ||Y||2). Отсюда, при ||X|| = ||Y|| = 1

4|Re(Ах, У)| £ 4m Þ| Re(Ах, У)| £ m.

Положим теперь (очевидно ||Y|| = 1):

.

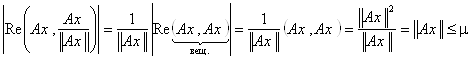Тогда , т. е. ||А|| £ m.

В 1) и 2) доказано, что ||А|| ³ m и ||А|| £ m, т. е. ||А|| = m = ▶

< Предыдущая		Следующая >