07.9. Спектр линейного оператора

Множество всех собственных значений линейного оператора Называется его спектром.

Спектр линейного оператора зависит от того каковы корни характеристического многочлена.

17°. В комплексном векторном пространстве V Каждый линейный оператор А имеет, по крайней мере, хотя бы один собственный вектор и следовательно в V Существует, по крайней мере, одно одномерное инвариантное относительно А подпространство.

◀ Справедливость этого следует из «основной теоремы алгебры». ▶

Более того j(l) = 0 в комплексном пространстве V имеет ровно N корней, с учетом их кратности: λ1, λ2, …, λN.

=

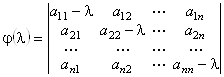С. С другой стороны

18°. λ1 + λ2 + … + λN = A11 + A11 + … + Ann = trA = SpA.

(trace) (Spur)

англ. нем.

◀ Величина A11 + A11 + … + Ann Называется следом матрицы А, но т. к. характеристический полином не зависит от выбора базиса то и SpA не зависит от базиса и Называется следом линейного оператора. ▶

19°. Для всякого линейного оператора А в вещественном пространстве размерности N >2 существует одномерное или двухмерное инвариантное подпространство.

◀ Если j(l) = 0 имеет хотя бы один вещественный корень λ0 то оператор А имеет собственный вектор и, следовательно, одномерное инвариантное относительно А подпространство.

Если j(l) = 0 не имеет вещественных корней, то существует комплексный корень l = a + bI. Решая относительно этого λ систему Az = lZ, найдем комплексное решение Z = X + Iy. Т. е.

A(X + Iy) = (a + IB)(X + Iy) = (aX – bУ) + I(bX + aY).

Приравнивая, вещественные и мнимые части правой и левой части равенства получим:. Отсюда ясно, что ℒ(X, Y) есть подпространство, инвариантное относительно оператора А. ▶

И, наконец, еще два утверждения о спектре линейного оператора.

20°. Если λ1, λ2, … , λN – все собственные значения оператора А, с учетом их кратностей и F(T) произвольный многочлен, то F(λ1), F(λ2), …, F(λN) – Это все собственные значения оператора F(А), причем кратность F(λI) такая же как и кратность λІ (собственные векторы при это не меняются).

Доказать самостоятельно.

21°. Если Ах = λ0Х и detA ¹ 0, то существует А–1 и кроме того .

◀ Ах = λ0Х. Действуем оператором А–1. А–1Аx = λ0А–1 Þ = А–1X. ▶

< Предыдущая		Следующая >