07.7 инвариантные пространства

Подпространство V1 пространства V Называется инвариантным относительно линейного оператора А если "XÎV1 Þ AxÎV1.

Примеры:

1) А – поворот вокруг оси Oz Обычного трехмерного пространства: Инвариантные подпространства: плоскость XOy и ось Oz.

2) А – ортогональное проектирование того же трехмерного пространства на плоскость XOy. Инвариантные подпространства: плоскость XOy, все плоскости проходящие через ось Oz, сама ось Oz, все прямые в плоскости XOy и проходящее через начало координат.

3) В пространстве Pn Многочленов степени не выше N, подпространства Pk "K, 0 £ K £ N инвариантны относительно оператора дифференцирования.

4) В любом пространстве V каждое подпространство инвариантно относительно тождественного и нулевого операторов.

5) В любом пространстве V само пространство V и подпространство, состоящее только из нулевого вектора {q} инвариантны относительно любого линейного оператора.

10°. Пересечение и сумма подпространств инвариантных относительно А Также инвариантны относительно А.

◀ Пусть V1 и V2 – инвариантны относительно А.

Пусть XÎV1∩V2Þ XÎV1, XÎV2 Þ AxÎV1, AxÎV2 Þ AxÎV1∩V2.

Пусть XÎV1 + V2 Þ X = U + V, UÎV1, VÎV2 Þ Ax = Au+ AvÞ AxÎV1 + V2 . ▶

11°. Если detA ¹ 0 и V1 инвариантно относительно оператора А, то V1 Инвариантно и относительно оператора А–1.

◀ Пусть Е1, Е2, … еn – базис V1 Þ Aе1, Aе2, … Aеn – принадлежат V1 (из инвариантности), линейно независимы и, следовательно, образуют базис в V1 Þ "AxÎV1

Х = a1Ae1 + a2Ae2 + … + aRAer Þ А–1x = А–1(a1Ae1 + a2Ae2 + … + aRAer) =

= a1E1 + a2E2 + … + aRErÎV1. ▶

12°. Пусть А Произвольный линейный оператор в V, (dimV = N) и пусть V = V1 ⊕ V2, где V1 и V2 – инвариантные подпространства оператора А. Пусть Е1, Е2, …, еr – базис в V1, Еr+1, Еr+2, …, еn – базис в V2. Тогда в силу инвариантности V1 и V2 относительно А:

Aei = a1IE1 + a2IE2 + … + aRiEr, I = 1, 2, …, R

Aei = aR+1, I Er+1 + … + aN i En, I = R + 1, R + 2, …, N.

И, следовательно, матрица линейного оператора А Имеет вид:

.

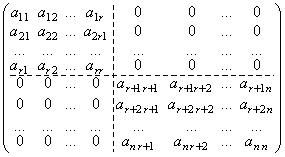Говорят, что матрица А имеет блочную структуру (распадается на клетки): .

< Предыдущая		Следующая >