07.6 Невырожденный линейный оператор

Линейный оператор А Называется невырожденным если N(A) º {q} т. е. Ax = q Þ X = q. (в нейтральный переходит только нейтральный).

6°. Если оператор А Невырожденный, то detA ¹ 0 для любого базиса.

◀ В самом деле, если Aij – элементы матрицы оператора А в некотором базисе и Sj Ее столбцы, то требование Ax = q Þ X = q можно записать в виде:

S1X1 + S2X2 + … + Snxn = 0 Þ X1 = X2 = … = Xn = 0,

Но это равносильно требованию линейной независимости столбцов матрицы оператора что (в свою очередь) равносильно требованию, что detA ¹ 0. ▶

7°. Если оператор А невырожденный, то существует и обратный ему линейный оператор А–1.

◀ Это следует из того что для невырожденной матрицы А существует обратная матрица и из взаимно однозначного соответствия между матрицами и линейными операторами. ▶

8°. Если к А существует обратный А–1, то detA ¹ 0.

◀ Ax = 0 (применим А–1), то: 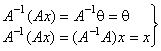Þ X = q. ▶

Если dimV = N и А невырожденный оператор то rangA = N, дефект оператора А равен нулю.

¢ 8°.Невырожденный оператор осуществляет взаимно однозначные соответствие R на R.

◀ Ax = Ay Þ Ax – Ay = A(X – Y) = q Þ X – Y = q Þ X = Y. ▶

9°. Если detA ¹ 0 то линейно независимые векторы переходят в линейно-независимые

векторы.

◀ Пусть E1, E2,…, En линейно независимые. Под действием А они переходят в Ae1, Ae2, …, Aen. Пусть a1Ae1 + a2Ae2 + … + aNAen = q Þ A(a1E1 + a2E2 + … + aNEn) = q Þ

(a1E1 + a2E2 + … + aNEn) = q Þ a1 + a2 + … + aN = 0. ▶

< Предыдущая		Следующая >