02.04. Ортогональные системы векторов
Def: Векторы X, YÎV называются ортогональными, если (Х, у) = 0.
1°. Если "YÎV, (X, Y) = 0 Þ X = q.
◀ Т. к. (X, Y) = 0 "Y, положим У = Х. Тогда (X, Х) = 0 Þ X = q. ▶
Система векторов ![]() Называется ортогональной, если (Fi, Fj) = 0 для I ¹ J (отметим, что (Fi, Fi) = |Fi|2).
Называется ортогональной, если (Fi, Fj) = 0 для I ¹ J (отметим, что (Fi, Fi) = |Fi|2).
Система векторов ![]() Называется ортонормированной, если
Называется ортонормированной, если![]() .
.
2°. Ортонормированная система векторов – линейно независима.
◀ ![]() – ортонормированна. Пусть a1E1 + a2E2 + …+ aNen = q. Умножим обе части равенства скалярно на Ej И получим: в левой части
– ортонормированна. Пусть a1E1 + a2E2 + …+ aNen = q. Умножим обе части равенства скалярно на Ej И получим: в левой части 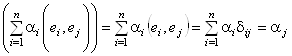 , а в правой части (q, Ej) = 0, т. е. aJ = 0. Равенство aJ = 0 для любого J означает линейную независимость ортогональной системы векторов. ▶
, а в правой части (q, Ej) = 0, т. е. aJ = 0. Равенство aJ = 0 для любого J означает линейную независимость ортогональной системы векторов. ▶
3°. В ортонормированном базисе скалярное произведение векторов есть сумма произведений одноименных координат.
◀ ![]() – ортонормированный базис
– ортонормированный базис ![]() . Тогда
. Тогда
 . ▶
. ▶
Следствие. В ортонормированном базисе ![]()
4°. В любом (конечномерном) евклидовом пространстве существует ортогональный базис.
◀ Пусть F1, F2, …, Fn базис в V. Покажем, что по указанному базису можно построить ортогональный базис (этот процесс называют Процессом ортогонализации).
А) E1 = F1;
Б) E2 = F2 + aE1 и a найдем из условия (E1, F1) = 0,
0 = (E1, E2) = (E1, F2) + a(E1, E2) Þ a = ![]() ;
;
В) E3 = F3 + aE1 + bE2 и a, b найдем из условий (E3, E1) = (E3, E2) = 0,
0 = (E1, E3) = (F3, E1) + a(E1, E2) Þ a = ![]() ,
,
0 = (E2, E3) = (F3, E2) + b(E2, E2) Þ b = ![]() ;
;
………………
………………
Г) ![]() . ▶
. ▶
Нормируя векторы ортогонального базиса получим ортонормированный базис пространства, т. е.
5°. В каждом евклидовом пространстве существует ортонормированный базис.
Процесс построения ортонормированного базиса, примененный в предыдущей теореме Называется процессом ортогонализации Штурма.
| < Предыдущая | Следующая > |
|---|