02.03. Длина вектора. Угол между векторами
А) Неравенство Коши-Буняковского (X, Y)2 £ (X, X)×(Y, Y).
◀ (aX – Y, aX – Y) = a2(X, X) – 2a(X, Y) + (X, Y) ³ 0, т. к. квадратный трехчлен относительно a сохраняет знак, то D £ 0 Þ 4(X, Y)2 – 4(X, X)(Y, Y) £ 0, (X, Y)2 £ (X, X)(Y, Y). ▶
Отметим, что равенство в неравенстве Коши-Буняковского достигается, если $a такое, что aX = Y, т. е. когда Х и У коллинеарны.
Частные случаи неравенства Коши-Буняковского:
А) 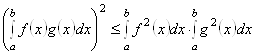 , б)
, б) ![]() .
.
Длиной вектора Х назовем величину |X| =![]() . (Неравенство Коши-Буняковского тогда запишется так: |(X, Y)|2 £ | X|2×|Y|2).
. (Неравенство Коши-Буняковского тогда запишется так: |(X, Y)|2 £ | X|2×|Y|2).
Расстоянием между двумя векторами Х и У назовем величину
![]() .
.
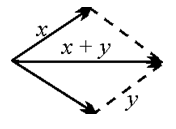
Б) Неравенство треугольника: |X + Y| £ | X| + |Y|.
◀ |X + Y|2 = (X + Y, X + Y) = (X, X)2 + 2(X, Y) + (Y, Y)2 = |X|2 + 2(X, Y) + + | Y |2 £ |X|2 + 2|X|×|Y| + | Y|2 = (|X| + |Y|)2. ▶
Углом между векторами Х и У назовем угол jÎ[0, p] такой, что ![]() .
.
Из неравенства Коши-Буняковского следует, что | cosj | £ 1.
| < Предыдущая | Следующая > |
|---|