01.19. Действия с подпространствами
Пусть L1 и L2 – подпространства пространства V.
L = L1 + L2 Û L º {X | X=X1 + X2, X1ÎL1, X2ÎL2}
N = L1∩L2 Û N º {X | XÎL1 Ù XÎL2}
![]() = L1∩L2 Û
= L1∩L2 Û ![]() º {X | XÎL1 Ú XÎL2}.
º {X | XÎL1 Ú XÎL2}.
Отметим, что теоретико-множественное объединение подпрост-ранств подпространством, вообще говоря, не является. Рисунок иллюстрирует, что сумма векторов из L1 + L2 не всегда принадлежит L1 + L2 .
30°. L = L1 + L2 и N = L1∩L2, где L1 и L2 – подпространства также являются подпростран-
Ствами.
◀ В доказательстве элементы подпространств L1 и L2 будем снабжать соответствующими индексами.
1) L = L1 + L2: "X, YÎL X + Y = (X1 + X2) + ( Y1 + Y2 )= (X1 + Y1) +(X2 + Y2);
xÎL: aX = a(X1 + X2) = aX1 +aX2; qL = ![]() = qV ; (–Х)=(–Х)1+(–Х)2 .
= qV ; (–Х)=(–Х)1+(–Х)2 .
2) N = L1∩L2 :  ;
; 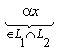 . ▶
. ▶
31°. Формула Грасмана dim(L1 + L2) = dimL1 + dimL2 – dimL1∩L2.
◀ Пусть dimL1∩L2 = K, dimL1 = K + L1, dimL2 = K + L2. Докажем, что dim(L1 + L2) = K + L1 + L2.
Пусть ![]() базис в L1∩L2. Дополним его до базиса L1:
базис в L1∩L2. Дополним его до базиса L1: ![]() и до базиса L2:
и до базиса L2: ![]() . Покажем, что
. Покажем, что ![]() ,
, ![]() базис в L1 + L2. Полнота:
базис в L1 + L2. Полнота:
X = X1 + X2 = ![]() =
= ![]() .
.
Линейная независимость (от противного).
Пусть a1E1 + … + aKek + b1F1 + … + ![]() + g1G1 + … +
+ g1G1 + … + ![]() = q;
= q;
![]()
Из последнего равенства следует, что векторы стоящие в его левой и правой частях принадлежат L1∩L2 . Тогда УÎL1∩L2 можно записать в виде: Y = d1E1 + … + dKek. Сравнивая Y = a1E1 + … + aKek + b1F1 + … + ![]() с Y = d1E1 +… + dKek, в силу единственности разложения У, заключаем, что a1 = d1, a2 = d2, …, aK = dK; b1 = b2 = … =
с Y = d1E1 +… + dKek, в силу единственности разложения У, заключаем, что a1 = d1, a2 = d2, …, aK = dK; b1 = b2 = … = ![]() Подставляя bI= 0 в (*) получаем a1E1 + … + aKek + g1G1 + …+
Подставляя bI= 0 в (*) получаем a1E1 + … + aKek + g1G1 + …+ ![]() = q и, в силу линейной независимости векторов E1, Е2, …, Ek, G1, G2,…,
= q и, в силу линейной независимости векторов E1, Е2, …, Ek, G1, G2,…, ![]() получаем: a1 = a2 =… = aK = g1 =… =
получаем: a1 = a2 =… = aK = g1 =… = ![]() = 0. ▶
= 0. ▶
| < Предыдущая | Следующая > |
|---|