01.18. Линейные многообразия

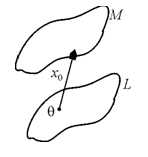
Пусть L – подпространство V, X0ÎV.

Множество M = {X | X = X0 + Y, YÎL} Называется линейным многообразием в V.

О линейном многообразии M говорят, что оно параллельно подпространству L и обозначают M = X0 + L.

Если X0ÎL, то M º L и M является подпространством. Если X0ÎV, но X0ÏL то линейное многообразие подпространством не является.

29°. Линейное многообразие порождается сдвигом единственного L.

◀ Пусть M = X0 + L и M = X¢0 + L¢. Тогда "XÎM

X = X0 + Y = X¢0 + Y¢ Þ Y = X¢0 + Y¢, где YÎL, Y¢ÎL¢. Так как это верно для "YÎL, положим Y = q. Получим Y¢ = X0 – X¢0 и т. к. Y¢ÎL¢ Þ X0 – X¢0 ÎL¢ . Тогда Þ YÎL¢. Итак, если YÎL Þ YÎL¢ Þ L Ì L¢, аналогично L Ì L¢, тогда L = L¢ . ▶

Размерность линейного многообразия – это размерность соответствующего подпространства L, базис линейного многообразия – это базис соответствующего подпространства. Забавный нюанс – базис линейного многообразия самому многообразию, вообще говоря, не принадлежит.

1-мерное многообразие называется прямой, K-мерное многообразие называется K-мер-ной плоскостью, (N – 1)-мерное многообразие – называется гиперплоскостью (N = dimV).

< Предыдущая		Следующая >