4.2. Метод исключений Гаусса
Решим рассмотренную ранее систему (пример 4.1) методом исключения Гаусса.
Пример 3.2. Решение проводиться в два этапа.
1 этап Прямой ход - матрица A преобразуется к треугольному виду: путем эквивалентных линейных преобразований уравнений системы поддиагональные коэффициенты матрицы А обнуляются.
x1 + 5×x2 - x3 = 2
x1 2×x3 = -1
2×x1 - x2 – 3×x3 = 5
Исключим x1 из 2-го и 3-го уравнения: ко 2-му уравнению прибавим 1-ое, умноженное на (-1); к 3-му уравнению прибавим 1-ое, умноженное на (-2).
X1 + 5×x2 - x3 = 2
- 5×x2 + 3×x3 = -3
- 11×x2 – x3 = 1
Исключим x2 из 3-го уравнения: к 3-му уравнению прибавим 2-ое, умноженное на (-11/5). Полученный вид системы после прямого хода
X1 + 5×x2 - x3 = 2
- 5×x2 + 3×x3 = -3
– 38/5×x3 = 38/5
2 этап Обратный ход - вычисляются значения неизвестных, начиная с последнего уравнения:
X3* = -1
-5×x2 + 3×x3*=-3 Þ x2*=(3 + 3×x3*)=(3 + 3×(-1))=0
X1 +5×x2* - x3*=2 Þ x1*=2 + 5×x2* + x3*=2 + 5×0 + (-1)=1
Полученное решение нужно обязательно проверить, подставив в исходную систему!
Словесное описание алгоритма метода исключения Гаусса. Схема алгоритма приведена на рисунках 4.1-4.6.
Алгоритм прямого хода:
Шаг 1. Примем k=1
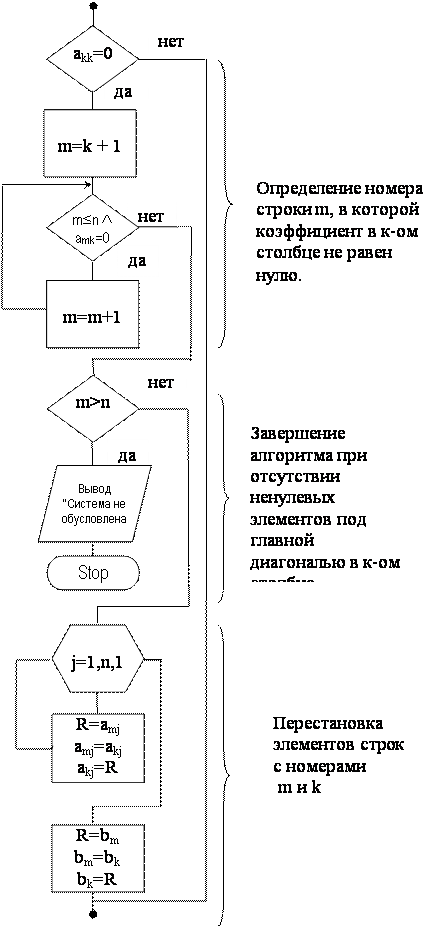
Шаг 2. Выбираем рабочую строку.
Если akk ≠ 0, то k-ая строка – рабочая.
Если нет, меняем k-ю строку на m-ю (n≥m>k), в которой amk ≠ 0, ![]() . Если такой строки нет, система вырожденная, решение прекратить.
. Если такой строки нет, система вырожденная, решение прекратить.
Шаг 3. Для строк i=k+1, k+2, …, n вычисляются новые значения коэффициентов.
 ,
, ![]() ,
, ![]() и новые правые части
и новые правые части ![]()
Шаг 4. Увеличиваем k = k + 1. Если k = n, прямой ход завершен, иначе алгоритм повторяется со второго шага.
Получаем верхнюю треугольную матрицу А:
 ,
, 
Алгоритм обратного хода:
Шаг 1. Вычислим ![]()
Шаг 2. Вычислим:
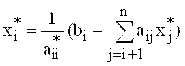 ,
, ![]()
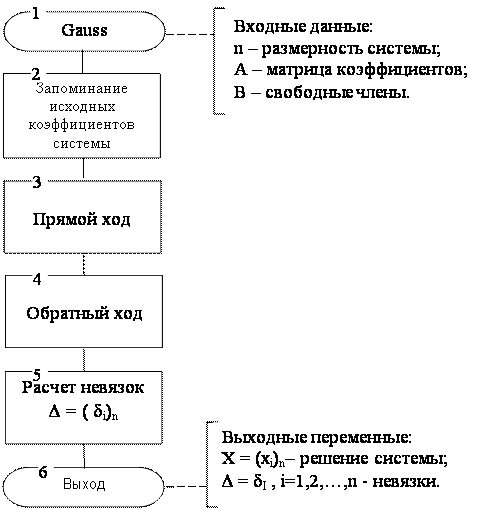 |
Рис. 4.1. Основной алгоритм решения СЛУ методом исключения Гаусса.
Для контроля правильности решения нужно считать невязки δi по формуле (4.5).
δi  ,
, ![]() (4.5)
(4.5)
Если невязки велики, задача решена неверно. Причиной может быть сбой машины (крайне редко), ошибки в программе, погрешность округления (при большом n и когда DA = detA = 0- система плохо обусловлена).
Разновидности метода исключения:
А) Метод исключения Гаусса с выбором главного элемента в столбце.
В алгоритме прямого хода на шаге 2 рабочая строка выбирается из условия
![]() ,
,
Т. е. рабочей выбирается та строка, в которой находится наибольший по модулю коэффициент k-го столбца, расположенный на главной диагонали и под ней.
Б) Метод Гаусса-Жордана.
В алгоритм прямого хода нужно внести следующие изменения:
- на шаге 3 ![]()
- на шаге 4 прямой ход завершиться при достижении условия k>n.
Вид матрицы коэффициентов после прямого хода

Упрощается обратный ход: xi =bi / ai, i, i =1,2,…,n
Недостаток метода – увеличение общего числа действий, и соответственно, влияния погрешности округления.
 |
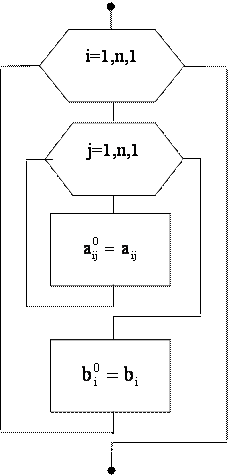 |
Рис. 3. Алгоритм запоминания коэффициентов.
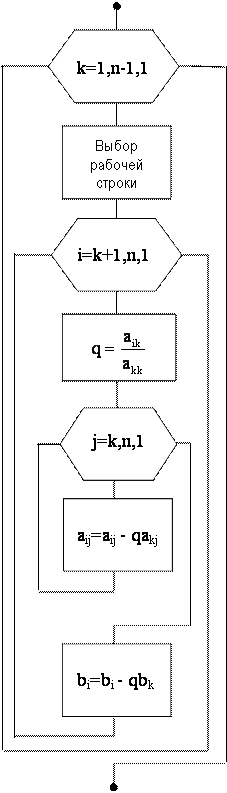
Рис. 4.2. Алгоритм прямого хода
 |
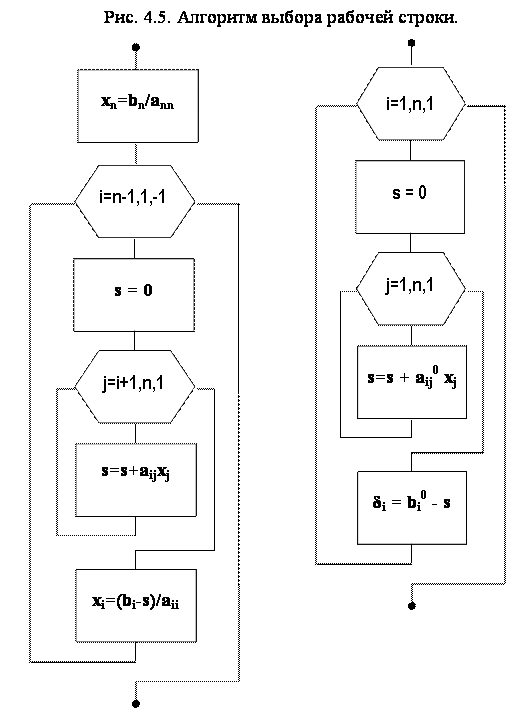 |
Рис. 4.6. Алгоритм расчета невязок
Рис. 4.5. Алгоритм обратного хода.
Нужно подчеркнуть, что для вычисления значения определителя квадратной матрицы можно использовать алгоритм прямого хода: для треугольной или диагональной квадратной матрицы определитель равен произведению элементов главной диагонали.
| < Предыдущая | Следующая > |
|---|