4.3. Метод простых итераций
Рассмотрим особенности решения СЛУ методом простых итераций на примере.
Пример 4.3. Требуется найти решение системы с точностью ε=0,001.
![]() x1 + 5×x2 - x3 = 2
x1 + 5×x2 - x3 = 2
x1 2×x3 = -1
2×x1 - x2 – 3×x3 = 5
Приведем систему к новому, Каноническому виду метода простых итераций. Для этого нужно преобразовать исходную систему так, чтобы в каждой строке новой матрицы А коэффициент, расположенный на главной диагонали, превышал по абсолютной величине сумму абсолютных значений остальных коэффициенты в этой сроке.
При выполнении эквивалентных линейных преобразований системы нужно соблюдать следующие требование: каждое уравнение исходной системы должно участвовать хотя бы в одном преобразовании.
В первом уравнении исходной системы коэффициент при х2 больше суммы модулей других коэффициентов: 5> 1+1. Поэтому это уравнение в новой системе нужно записать вторым уравнением. Для получения нового первого уравнения можно второе уравнение умножить на 2 и сложить с третьим уравнением. Для получения нового третьего уравнения можно из третьего уравнения вычесть второе.
В итоге описанных преобразований получиться следующая система:
![]()
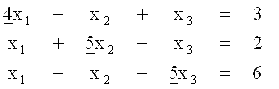
Важно отметить, что подобные преобразования не меняют решения системы.
Выразим явно из каждого Нового уравнения очередное неизвестное – получим формулы итерационного процесса.
![]()
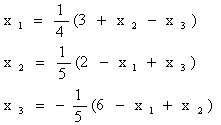
![]()
Возьмем Любое начальное приближение ![]() , например
, например ![]() .
.
Вычислим новое приближение решения ![]() , подставив в правую часть
, подставив в правую часть ![]() начальное приближение:
начальное приближение:

![]()
![]()
Оценим достигнутую точность δ по формуле:
![]()
Итерационный процесс нужно продолжить, т. к. δ > ε.
Вычислим второе приближение ![]() , подставив в правую часть
, подставив в правую часть ![]() первое приближение:
первое приближение:

![]()
Третье приближение:
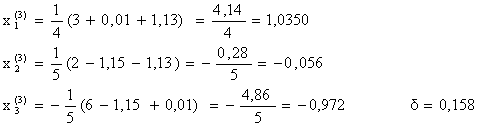
Четвертое приближение:
![]()
Очевидно, что итерационный процесс сходиться, т. к. значение δ монотонно убывает. Для достижения требуемой точности ε=0,001 потребуется еще несколько итераций.
Скорость сходимости зависит от уровня преобладания значений диагональных коэффициентов.
Основные расчетные зависимости метода простых итераций:
Формула итерационного процесса:
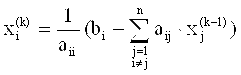 ,
, ![]() (4.6)
(4.6)
Где: k = 1, 2, … – номер приближения.
![]() – начальное приближение,
– начальное приближение, ![]() ;
;
Условия завершения итерационного процесса:
D£e (4.7)
Где e – требуемая точность;
D – оценка достигнутой точности, ![]() (4.8)
(4.8)
Или 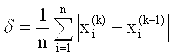 (4.9)
(4.9)
Условие сходимости итерационного процесса (условие преобладания диагональных коэффициентов):

![]() (4.10)
(4.10)
Схема алгоритма метода представлена на рис. 4.7.
Если в полученных результатах значения δ > e и k > kmax, то задача не решена, т. е. x(1:n) не является решением системы. Необходимо проверить условия сходимости или увеличить kmax.
| < Предыдущая | Следующая > |
|---|