4.1. Формулы Крамера
Xi* = DAI / DA, I = 1, N, 1 (4.4)
Где Ai – вспомогательная матрица, полученная из A заменой i-го столбца вектором свободных членов.
Пример 4.1. Решить СЛУ, используя формулы Крамера.
![]() x1 + 5×x2 - x3 = 2
x1 + 5×x2 - x3 = 2
x1 2×x3 = -1
2×x1 - x2 – 3×x3 = 5
Вычислим определители по правилу треугольников:
DA = 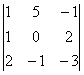 = 0 + 1 + 20 + 0 + 15 + 2 = 38 – система обусловлена.
= 0 + 1 + 20 + 0 + 15 + 2 = 38 – система обусловлена.
DA1 = 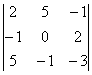 = 0 + 50 - 1 - 0 + 4 - 15 = 38
= 0 + 50 - 1 - 0 + 4 - 15 = 38
DA2 = 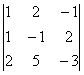 = 3 + 8 – 5 – 2 + 6 - 10 = 0
= 3 + 8 – 5 – 2 + 6 - 10 = 0
DA3 =  = 0 - 10 – 2 – 0 -25 - 1 = -38
= 0 - 10 – 2 – 0 -25 - 1 = -38
Вычислим решения:
X1* = DA1 / DA = 38/38 = 1;
X2* = DA2 / DA = 0/38 = 0;
X3* = DA3 / DA =-38/38 = -1.
Проверим полученное решение подстановкой в исходную систему.
1 + 5×0 – (-1) = 2
1 + 2×(-1) = -1
2×1 – 0 – 3×(-1) = 5
Система обращается в тождество, решение верное.
Формулы Крамера применяться редко, только для n≤4.
| < Предыдущая | Следующая > |
|---|