3.2.1. Метод простых итераций (метод последовательных приближений)
Метод реализует стратегию постепенного уточнения значения корня.
Постановка задачи. Дано нелинейное уравнение (3.1). Корень отделен x* Î [a;b]. Требуется уточнить корень с точностью ε.
Уравнение ( 3.1) преобразуем к эквивалентному виду x=φ(x), (3.7)
Что можно сделать всегда и притом множеством способов.
Выберем начальное приближение x0Î [a;b].
Вычислим новые приближения:
X1=φ(x0)
X2=φ(x1)
………..
Xi=φ(xi-1) , i=1,2,… где i − номер итерации. (3.8)
Последовательное вычисление значений xi по формуле (3.8) называется итерационным процессом метода простых итераций, а сама формула - формулой итерационного процесса метода.
Если ![]() , то итерационный процесс Сходящийся .
, то итерационный процесс Сходящийся .
Условие сходимости ![]() (3.9)
(3.9)
Точное решение x* получить невозможно, так как требуется Бесконечный Итерационный процесс.
Можно получить Приближенное Решение, прервав итерационный (3.8) при достижении условия
![]() , (3.10)
, (3.10)
Где ε - заданная точность; i - номер последней итерации.
В большинстве случаев условие завершения итерационного процесса (3.10) обеспечивает близость значения xi к точному решению:
![]()
Рассмотрим геометрическую иллюстрацию метода простых итераций.
Уравнение (3.7) представим на графике в виде двух функций: y1 = x и y2= φ(x).
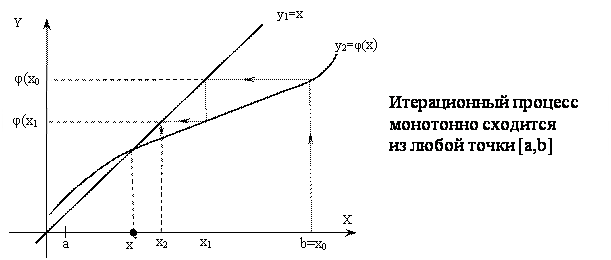
Возможные случаи взаимного расположения графиков функций, и соответственно, видов итерационного процесса показаны на рис. 3.7 – 3.10.
Рис. 3.7 Итерационный процесс для случая 0<![]() <1
<1 ![]() xÎ[a, b].
xÎ[a, b].
 |
Рис. 3.8 Итерационный процесс для случая -1<![]() <1
<1 ![]() xÎ[a, b].
xÎ[a, b].
 |
Рис. 3.9 Итерационный процесс для случая ![]() >1
>1 ![]() xÎ[a, b].
xÎ[a, b].
 |
Рис. 3.10 Итерационный процесс для случая ![]() £ - 1
£ - 1 ![]() xÎ[a, b].
xÎ[a, b].
Из анализа графиков следует, что скорость сходимости растет при уменьшении значения ![]()
Метод достаточно прост, обобщается на системы уравнений, устойчив к погрешности округления (она не накапливается).
При разработке алгоритма решения нелинейного уравнения методом простых итераций следует предусмотреть защиту итерационного процесса от зацикливания: использовать в качестве дополнительного условия завершения итерационного процесса превышение заданного максимального числа итераций.
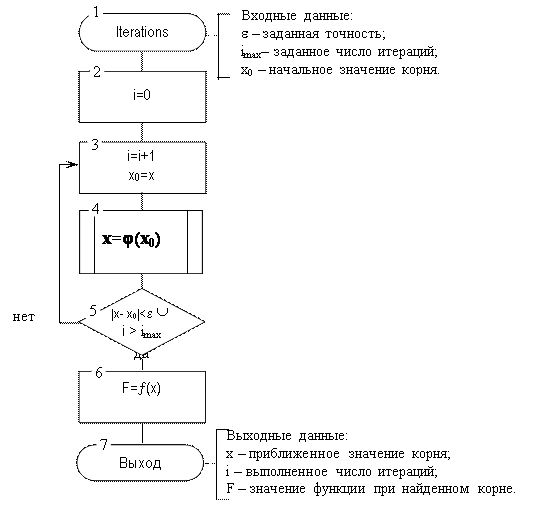 |
Рис 3.11. Алгоритм решения нелинейного уравнения методом
простых итераций:
Основной проблемой применения метода является обеспечение сходимости итерационного процесса: нужно найти такое эквивалентное преобразование (3.1) в (3.7), чтобы обеспечивалось условие сходимости (3.9) .
Простейшие эквивалентные преобразования, например:
F(x) = 0 => x+f(x) = x, т. е. φ(x) = x + f(x)
Или выразить явно x из (3.1)
F(x) = 0 => x - φ(x) = 0 => x = φ(x)
Не гарантируют сходимость.
Рекомендуется следующий способ получения формулы Сходящегося итерационного процесса.
Пусть ![]() .
.
Если это не так, переписать уравнение (3.1) в виде
![]()
Умножить обе части уравнения на ![]() и к обеим частям прибавить x:
и к обеим частям прибавить x:
![]()
Константу l вычислить по формуле:
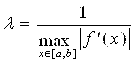 (3.11)
(3.11)
Такое значение λ гарантирует сходящийся итерационный процесс по формуле
Xi = xi+1− λ f(x) (3.12)
Где i=1,2,… - номер итерации, x0Î[a, b] – начальное приближение.
Пример 3.2.
Методом простых итераций уточнить корень уравнения x3=1-2 x с точностью ε=0,001. Корень отделен ранее (см. пример 3.1), x* Î [0;1].
Сначала нужно получить формулу сходящегося итерационного процесса.
Из уравнения выразим явно x:
![]()
Проверим условия сходимости для полученной формулы:
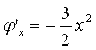 ,
, ![]() ,
, ![]()
![]() для x Î (0;1].
для x Î (0;1].
Условие сходимости не соблюдается, полученная формула не позволит уточнить корень.
Воспользуемся описанным выше способом получения формулы итерационного процесса (формулы 3.11, 3.12).
![]() ,
, ![]() ,
, ![]() для всех x Î [0;1].
для всех x Î [0;1].
Наибольшее значение ![]() принимает при x = 1, т. е.
принимает при x = 1, т. е.
![]()
Следовательно ![]() .
.
Формула Сходящегося итерационного процесса
![]()
Уточним корень с помощью данной формулы.
Выберем начальное приближение на [0;1], например x0=0,5 (середина отрезка).
Вычислим первое приближение ![]()
![]()
Проверим условие завершения итерационного процесса
![]()
Расчет следует продолжить.
![]()
![]()
![]()
![]()
X3 = 0,458216
X4 = 0,455688
X5 = 0,454488
X6 = 0,453917 − ответ, т. к. ![]()
Проверим полученное значение, подставив в исходное уравнение:
![]()
Значение f(x) близко к 0 с точностью, близкой к ε, следовательно, корень уточнен правильно.
| < Предыдущая | Следующая > |
|---|