3.2.2. Метод Ньютона (касательных)

Постановка задачи.

Дано нелинейное уравнение (3.1) f(x)=0. Корень отделен x* Î [a;b]. Требуется уточнить корень с точностью ε.

Метод основан на стратегии постепенного уточнения корня. Формулу уточнения можно получить из геометрической иллюстрации идеи метода.

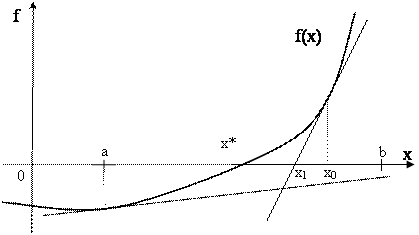
Рис. 3.12. Геометрическая иллюстрация метода Ньютона.

На отрезке существования корня выбирается начальное приближение x0. К кривой f(x) в точке А с координатами (x0, f(x0)) проводится касательная. Абсцисса x1 точки пересечения этой касательной с осью ОХ является новым приближением корня.

Из рисунка следует, что x1 = x0 − CB

Из ∆ABC: CD=. Но .

Следовательно,

Аналогично, для i-го приближения можно записать формулу итерационного процесса метода Ньютона:

, где x0 Î [a;b]. (3.13)

Условие окончания расчета: , (3.14)

Где 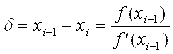−корректирующее приращение или поправка.

Условие сходимости итерационного процесса:

(3.15)

Если на отрезке существования корня знаки и не изменяются, то начальное приближение, обеспечивающее сходимость, нужно выбрать из условия

, x0Î[a;b]. (3.16)

Т. е. в точке начального приближения знаки функций и ее второй производной должны совпадать.

Рис. 3.13. Геометрическая иллюстрация выбора начального приближения: график f(x) вогнутый, , тогда x0=b, т. к. f(b)>0.

Если же выбрать x0=a, то итерационный процесс будет сходиться медленнее или даже расходиться (см. касательную для x0=a).

●

Рис. 3.14. Геометрическая иллюстрация выбора начального приближения: график f(x) выпуклый, f ’’(x)<0 , тогда x0 =a, т. к. f(a)<0.

Метод Ньютона в отличие от ранее рассмотренных методов используют свойства функции в виде значения производной, что значительно ускоряет итерационный процесс. При этом, чем больше значение модуля производной в окрестности корня (чем круче график функции), тем быстрее сходимость.

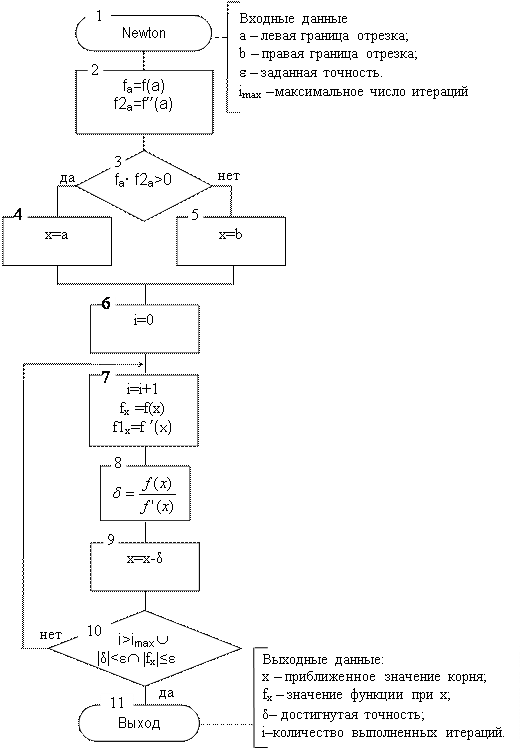Рис 3.15. Схема алгоритма метода Ньютона:

Достоинства метода: высокая скорость сходимости; обобщается на системы уравнений.

Недостатки: сложный, т. к. требуется вычисление производных; сильная зависимость сходимости от вида функции и выбора начального приближения.

Пример 3.3.

Методом Ньютона уточнить корни уравнения x3 = 1− 2x с точностью ε=0,001. Корень отделён ранее (пример 3.1), x* Î [0,1].

Сначала нужно выбрать начальное приближение.

F(x) = x3+ 2 x−1

F ’(x) = 3 x2 +2

F ’’(x) = 6 x

Производные имеют постоянный знак на отрезке (0,1], поэтому для выбора начального приближения достаточно использовать условие (3.16).

Знак второй производной на отрезке положительный, следовательно

X0 = b = 1, т. к. f(b) = f(1) = 13+2·1−1 = 2 > 0

Вычислим несколько приближений:

X1 =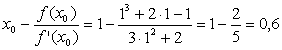

X2 =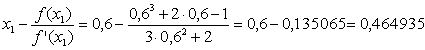

X3 =0,464935−0,011468=0,453467

X3 =0,453463−0,0000695=0,453398

Решение получено за 4 итерации, так как поправка стала меньше заданной точности: 0,0000695 < ε.

< Предыдущая		Следующая >