3.2. Алгоритмы уточнения корней уравнения. Метод дихотомии (половинного деления, бисекций)

Уточнение корня – это вычисление интересующего корня с заданной точностью e.

Приближённые значения корней уравнения, полученные на предыдущем этапе, уточняются различными итерационными методами.

Рассмотрим некоторые из них.

Постановка задачи:

Дано нелинейное уравнение ¦(x) = 0.

Корень отделен, т. е. известно, что x* Î [a, b].

Требуется вычислить корень с заданной точностью ε.

Метод реализует стратегию постепенного уменьшения отрезка существования корня, используя факт изменения знака функции в окрестности корня.

Алгоритм метода.

1. Вычислить координату середины отрезка [a, b] x = (a+b)/2 и значение ¦(x) в этой точке.

2. Уменьшить отрезок, отбросив ту его половину, на которой корня нет.

Если знак функции в начале отрезка и в его середине одинаков, то корень находится на второй половине, первую половину можно отбросить, переместив начало отрезка в его середину:

Если ¦(a) ·¦(x)>0 => x*Î [x, b] => a=x, иначе x*Î [a, x] => b=x

3. Проверить условие завершения вычислений : длина отрезка не превышает заданную точность и значение функции близко к 0 с заданной точностью:

B-a ≤ ε ∩ |¦(x)| ≤ ε.

Если условие достигнуто, расчет завершен, иначе повторить алгоритм сначала.

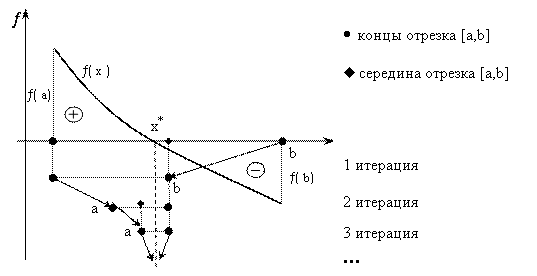
Рис. 3.4 Геометрическая иллюстрация метода бисекций.

B=x

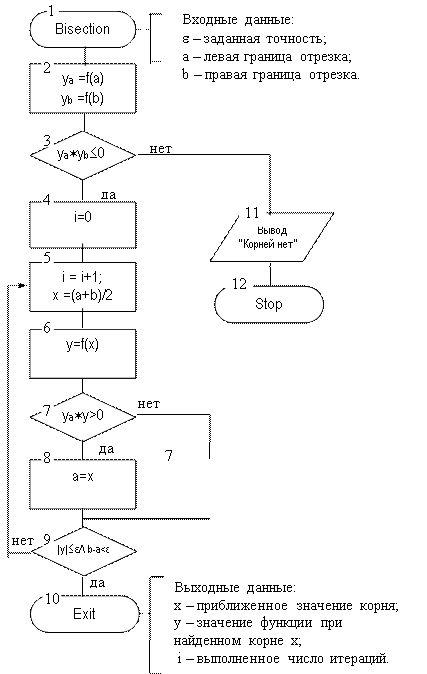
Рис. 3.5 Схема алгоритма метода бисекций (дихотомии)

Количество итераций n, требуемых для достижения требуемой точности ε можно оценить заранее из соотношения

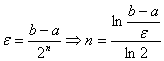(3.6)

Метод дитохомии − простой и надежный метод поиска простого корня любой функции, устойчивый к погрешности округления. Даже если на отрезке есть несколько корней (нечетное количество),то будет найден один из них.

Недостатки метода: скорость сходимости низкая, не обобщается на систему уравнений.

Метод дихотомии нельзя использовать для уточнения не простого корня − корень совпадает с точкой экстремума функции, т. к. в этом случае функция не изменяет свой знак в окрестности корня.

Рис. 3.6. Непростой корень уравнения.

Пример 3.1. Требуется решить уравнение x3+2x=1

Сначала нужно отделить решения.

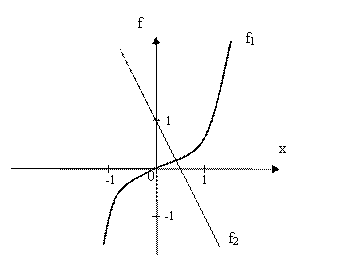Удобно записать уравнение в виде x3=1-2x и построить графики двух элементарных функций ¦1(x)= x3 и ¦2(x)=1-2x

Рис. 3.7 Отделение корней уравнения x3 = 1 - 2 x.

Из графика следует, что корень один: x* Î [0;1].

Проверим наличие корня на отрезке

¦(a) = ¦(0) = 03+2·0 = -1, ¦(b) = ¦(1) = 13+2·1 = 2

Знаки на концах отрезка разные, следовательно, корень отделен верно.

Выполним несколько итераций уточнения корня.

1 итерация. Середина отрезка x = ( 0 + 1) / 2 = 0,5

Значение функции в середине ¦(x)=¦(0,5)= 0,53+2·0,5-1=0,125>0

Функция меняет свой знак на первой половине отрезка, следовательно, корень на первой половине, поэтому отбросим вторую половину, переместив конец отрезка в середину: x* Î [0;0,5]

2 итерация. Середина отрезка x = ( 0 + 0,5) / 2 = 0,25

Значение функции в середине

¦(x)=¦(0,25)= 0,253+2·0,25-1=0,0115625-0,5=-0,484375

Функция не меняет свой знак на первой половине отрезка, поэтому отбросим ее: x* Î [0,25;0,5]

Вычисления следует продолжить до достижения требуемой точности. Например, если ε=0,001 то потребуется не менее 10 итераций:

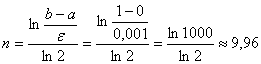
< Предыдущая		Следующая >