4.3. Спряжені простори

Нехай лінійний нормований простір. Позначимо через множину всіх неперервних лінійних функціоналів на . Множина так само є лінійним нормованим простором. Дійсно, якщо , то їх сумою є функція така, що . Якщо і , то є функціоналом . Норма в задається формулою (4.2)

.

Неважко показати, що всі властивості норми виконуються. Простір нази-вається Спряженим З простором .

Теорема 4.2. Спряжений простір завжди повний.

Таким чином, не зважаючи на властивості , простір банахів. Крім того, , де – поповнення простору . Рівність мається на увазі з точністю до ізоморфізму.

Приклад 4.5. Нехай – -вимірний простір. Різні норми в індукують різні норми в. Ось кілька прикладів пар відповідних одна одній норм
в і :

A) , ;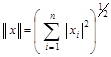

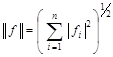B) , , , ;

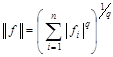C) , ;

D) , .

Тут – координати вектора у базисі , – координати вектора у базисі Базиси в і мають зв’язок

Такі базиси називаються двоїстими.

Приклад 4.6. Розглянемо простір усіх збіжних до нуля послідовностей з нормою . Спряженим до нього є простір абсолютно всіх сумованих послідовностей з нормою .

Приклад 4.7. Простір ізоморфний простору , складеному з усіх обмежених послідовностей з нормою .

Приклад 4.8. Нехай . Розглянемо простір всіх послідовностей з нормою

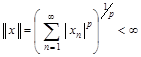
Спряжений простір ізоморфний , де . Загальний вигляд лінійного функціоналу

, , .

Аналогічно, спряжений до простір ізоморфний , де . Загальний вигляд функціоналу

, , .

Теорема 4.2. Нехай – дійсний гільбертів простір. Для будь-якого неперервного лінійного функціоналу на існує єдиний елемент такий, що

, , (4.3)

Причому . Навпаки, якщо , то формула (4.3) визначає такий неперервний лінійний функціонал , що . Таким чином, формула (4.3) визначає ізоморфізм між просторами і .

Сформульована теорема має аналог і в комплексному випадку. Таким чином, у гільбертовому випадку спряжені простори повністю описано.

Розглянемо другий спряжений простір . Зазначимо, що кожен елемент визначає деякий лінійний функціонал на . Дійсно, припустимо

,

Де . Очевидно, що є неперервним лінійним функціоналом на . Тому . Якщо , то простір називається Рефлексивним.

Простори з прикладів 4.5, 4.8 рефлексивні. Простір із прикладу 4.6 не є рефлексивним.

< Предыдущая		Следующая >