3.3. Евклідові простори

Визначення 3.4. Скалярним добутком у дійсному лінійному просторі називається дійсна функція , визначена для кожної пари елементів , яка задовольняє умовам:

1);

2);

3);

4), причому тільки при .

Лінійний простір із введеним у ньому скалярним добутком називається Евклідовим простором.

Визначення 3.5. Повний евклідів простір нескінченного числа вимірів називається Гільбертовим.

В евклідовому просторі вводиться норма за допомогою формули

.

Справедлива нерівність Коші-Буняковського

.

Наявність скалярного добутку дозволяє ввести не тільки довжину вектора (норму), але й кут між векторами. Кут між і визначається за формулою

.

Якщо , тобто , то вектори і називаються Ортого-нальними.

Система ненульових векторів називається Ортогональною, якщо при .

Якщо вектори ортогональні, то вони лінійно незалежні.

Якщо ортогональна система є повною, тобто найменший простір, який її містить, співпадає з усім простором , то вона називається Ортогональним базисом. Якщо

То вона називається Ортогональною нормованою або Ортонормованою. Зрозуміло, що якщо ортогональна, то буде ортонормованою.

Приклад 3.19. -вимірний простір зі скалярним добутком

,

Де , є добре відомим прикладом евклідового простору.

Ортонормований базис (один із нескінченного числа можливих) утворює вектори

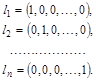
Приклад 3.20. Простір зі скалярним добутком

Є гільбертовим простором. Найпростіший ортонормований базис утворюють вектори

Приклад 3.21. Простір неперервних функцій зі скалярним добутком

Є евклідовим простором, але не гільбертовим, оскільки він не повний. Серед різних ортогональних базисів найважливішим є тригонометрична система

, , , .

Приклад 3.22. Простір функцій, інтегрованих з квадратом і з тим самим скалярним добутком, що й у прикладі 3.21, є гільбертовим простором. Ортогональним базисом у ньому служить та сама тригоно-метрична система, що й у прикладі 3.21.

Має місце наступний факт. У сепарабельному евклідовому просторі будь-яка ортогональна система не більше ніж зліченна. Зазначимо, що всі простори у прикладах 3,20 – 3,22 сепарабельні.

Теорема 3.1. (Про ортогоналізацію). Нехай

Лінійно незалежна система векторів в евклідовому просторі . Тоді в існує система елементів

, (3.3)

Яка задовольняє умовам:

1) система (3.3) ортонормована;

2) кожен елемент можна представити у вигляді

,

Причому ;

3) кожен елемент можна представити у вигляді

,

Причому .

Наслідок 3.1. У сепарабельному евклідовому просторі завжди існує ортонормований базис.

Визначення 3.6. Два евклідові простори і називаються Ізоморф-ними, якщо існує таке взаємно однозначне відображення в , що вико-нуються умови:

1);

2);

3).

Теорема 3.2. Будь-який сепарабельний гільбертів простір ізоморфний простору .

Таким чином, простір функцій , який розглядався в прикладі 3.22, ізоморфний простору послідовностей .

Справедливе твердження: для того, щоб нормований простір був евклі-довим, необхідно й достатньо, щоб для будь-яких виконувалась рівність

.

Ця рівність не виконується для , , , , .

< Предыдущая		Следующая >