3.2. Поняття норми

Визначення 3.3. Нехай – лінійний простір. Відображення, яке зіставляє кожному елементу число , називається Нормою, якщо виконуються такі умови:

1), причому тоді й тільки тоді, коли ;

2), ;

3), де , – число.

Лінійний простір, у якому задана деяка норма, називається Нормованим. Будь-який нормований простір стає метричним, якщо в ньому ввести відстань

. (3.2)

Повний нормований простір називається Банаховим простором або -прос-тором.

Приклад 3.12. Пряма лінія стає нормованим простором, якщо вважати .

Простори можна зробити нормованими, а потім увести відстань за фор-мулою (3.2). Наведемо кілька прикладів.

Приклад 3.13. У дійсному -вимірному просторі впровадимо

.

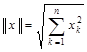Приклад 3.14. У просторі впровадимо

.

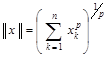Приклад 3.15. У просторі впровадимо

.

Приклад 3.16. У просторі впровадимо

.

Приклад 3.17. У просторі обмежених послідовностей впровадимо

.

Приклад 3.18. У просторі впровадимо

.

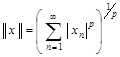Раніше було визначено поняття підпростору. У нормованих просторах най-важливішими є Замкнені підпростори. У скінченновимірному нормованому просторі будь-який підпростір замкнений. У нескінченновимірному випадку це не так. Наприклад, у підпростір не замкнений.

Таким чином, Підпростором нормованого простору називаються тільки замкнені підпростори. Довільний підпростір, який може бути не замкненим, називають лінійним многовидом.

Підпростором, що породжений множиною елементів , називають найменший замкнений простір, який містить . Інакше він називається Лінійним замиканням множини .

Систему елементів, яка лежить у нормованому просторі , називають Повною, якщо породжений нею підпростір (замкнений), співпадає з усім . Наприклад, в силу теореми Вейерштрасса сукупність функцій

Є повною у просторі неперервних функцій .

< Предыдущая		Следующая >