2.6. Компактність у метричному просторі

У метричних просторах існують досить конструктивні критерії компакт-ності. В метричному випадку компактність тісно пов’язана з поняттям цілком обмеженості.

Нехай – підмножина метричного простору з метрикою . Множи-на називається -сіткою для , якщо для будь-якої точки існує точка така, що

.

Множина не обов’язково міститься в . Вона може навіть мати з порожній перетин. Однак, маючи для деяку -сітку , можна побудувати -сітку .

Наприклад, цілочислові точки утворюють на площині -сітку.

Множина називається Цілком обмеженою, якщо для неї при будь-якому існує Скінченна -сітка.

Цілком обмежена множина повинна бути обмеженою. Обернений висно-вок може бути неправильним.

Очевидно, що якщо множина цілком обмежена, то і її замикання теж цілком обмежене.

Теорема 2.16. Для того, щоб множина , яка лежить у повному метрич-ному просторі, була передкомпактною, необхідно і достатньо, щоб вона була цілком обмеженою.

Таким чином, у повних метричних просторах замкнені цілком обмежені множини будуть компактними.

Приклад 2.6. У просторі компактними є замкнені обмежені множини й тільки вони.

Приклад 2.7. Одинична сфера в

Є обмеженою, але не цілком обмеженою множиною. Тому, не зважаючи на те, що замкнена, вона не є компактною. Дійсно, розглянемо точку з вигляду

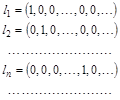
Відстань між будь-якими і , дорівнює . Тому для не може бути -сітки при .

У цьому ж просторі розглянемо множину всіх точок таких, що , , …, , … . Ця множина називається основним паралелепіпедом або гільбертовою цеглиною. Можна показати, що вона цілком обмежена, а оскільки вона є замкненою, то – компакт.

Приклад 2.8. Розглянемо критерій передкомпактності у просторі .

Сім’я функцій , визначених на , називається Рівномірно обме-женою, якщо існує таке число , що

Для всіх , .

Сім’я називається Одностайно неперервною, якщо для кожного знайдеться таке, що

Для всіх таких, що для всіх .

Теорема 2.17. (Арцела). Для того, щоб сім’я була передкомпактною
у , необхідно й достатньо, щоб вона була рівномірно обмеженою і одностайно неперервною.

Теорема Арцела використовується для доведення теореми Пєано про існування розв’язку диференціального рівняння. У теоремі Пєано йдеться про те, що розв’язок диференціального рівняння існує, якщо функція неперервна. При цьому не потрібна ліпшицевість функції по , але й не гарантується єдиність розв’язку.

На випадок метричних просторів можна перенести поняття рівномірної неперервності.

Відображення , де – метричний простір з метрикою і – метричний простір з метрикою , називається Рівномірно неперервним, якщо для будь-якого існує таке , що як тільки . Тут залежить тільки від і не залежить від , .

Теорема 2.18. Неперервне відображення метричного компакту в мет-ричний простір є рівномірно неперервним.

< Предыдущая		Следующая >