3.3. Точечные оценки параметров распределения

На практике часто удается предсказать или оценить с помощью гистограммы вид распределения наблюдаемой случайной величины ξ с точностью до неизвестного параметра (или нескольких параметров). Одной из основных задач математической статистики является нахождение оценки (приближенного значения) неизвестного параметра по имеющейся выборке.

Основные понятия

Пусть наблюдается случайная величина ξ с функцией распределения и плотностью распределения . Случайная выборка представлена вектором с реализацией . (3.7)

Параметром распределения случайной величины называется любая числовая характеристика этой случайной величины (математическое ожидание, дисперсия и т. п.) или любая константа, явно входящая в выражение для функции или плотности распределения.

Если параметр неизвестен, то его точечной оценкой называется произвольная функция элементов выборки

. (3.8) Реализацию оценки, т. е. значение оценки для наблюдавшейся в эксперименте реализации выборки, принимают за приближенное значение неизвестного параметра

Из соотношения (3.8) видно, что как функция случайных величин сама также является случайной величиной. Закон распределения оценки зависит от вида функции , числа наблюдений и значения оцениваемого параметра.

Ясно, что существует много разных способов построения точечной оценки, и не всякая зависимость может давать удовлетворительную оценку неизвестного параметра . Рассмотрим некоторые свойства, которыми должна обладать оценка, чтобы ее можно было считать хорошим приближением к неизвестному параметру.

Оценка параметра называется Несмещенной, если ее математическое ожидание равно оцениваемому параметру, то есть

. (3.9)

Если свойство (2.2) не выполняется, то есть

, (3.10)

То оценку называют Смещенной, при этом величину называют систематической ошибкой оценки .

Требование несмещенности означает, что выборочные значения оценок, полученных в результате повторения выборок, группируются около оцениваемого параметра.

Оценка параметра называется Состоятельной, если при она сходится по вероятности к оцениваемому параметру , т. е. для любого ε > 0 выполняется равенство

. (3.11)

Следующая теорема устанавливает достаточные условия состоятельности оценки параметра .

Теорема. Если при и , то оценка параметра является состоятельной.

Состоятельность оценки означает, что, при достаточно большом объеме выборки с вероятностью близкой к единице, отклонение оценки от истинного значения параметра меньше ранее заданной величины.

Обычно в качестве Меры точности оценки используется среднеквадратическая ошибка (среднее значение квадрата ошибки) 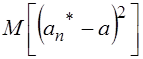. Очевидно, чем меньше эта ошибка, тем теснее сгруппированы значения оценки около оцениваемого параметра. Поэтому всегда желательно, чтобы ошибка оценки была по возможности малой. Используя свойства математического ожидания, нетрудно получить

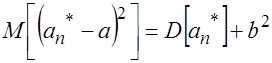. (3.12)

Для несмещенных оценок

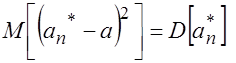, (3.13)

То есть их мерой точности является дисперсия.

Несмещенная оценка параметра называется его Эффективной Оценкой, если ее дисперсия является наименьшей среди дисперсий всех возможных оценок параметра , вычисленных по одному и тому же объему выборки.

Точечные оценки математического ожидания и дисперсии

Пусть случайная выборка порождена наблюдаемой случайной величиной ξ, математическое ожидание и дисперсия которой неизвестны. В качестве оценок для этих характеристик было предложено использовать выборочное среднее

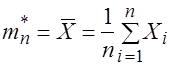
И выборочную дисперсию

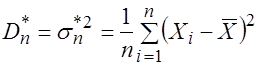. (3.14)

Рассмотрим некоторые свойства оценок математического ожидания и дисперсии.

1. Вычислим математическое ожидание выборочного среднего:

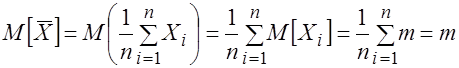. (3.15)

Следовательно, выборочное среднее является несмещенной оценкой для .

2. Напомним, что результаты наблюдений – независимые случайные величины, каждая из которых имеет такой же закон распределения, как и величина , а значит, , , . Будем предполагать, что дисперсия конечна. Тогда, согласно теореме Чебышева о законе больших чисел, для любого ε > 0 имеет место равенство ,

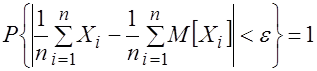Которое можно записать так: 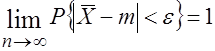. (3.16) Сравнивая (3.16) с определением свойства состоятельности (3.11), видим, что оценка является состоятельной оценкой математического ожидания .

3. Найдем дисперсию выборочного среднего:

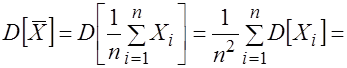
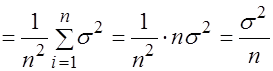. (3.17)

Таким образом, дисперсия оценки математического ожидания уменьшается обратно пропорционально объему выборки.

Можно доказать, что если случайная величина ξ распределена нормально, то выборочное среднее является эффективной оценкой математического ожидания , то есть дисперсия принимает наименьшее значение по сравнению с любой другой оценкой математического ожидания. Для других законов распределения ξ это может быть и не так.

Выборочная дисперсия является смещенной оценкой дисперсии , так как 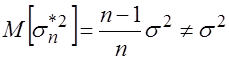. (3.18)

Действительно, используя свойства математического ожидания и формулу (3.17), найдем

.

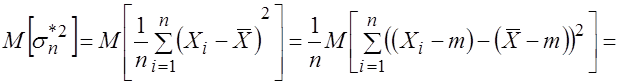
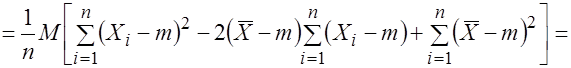
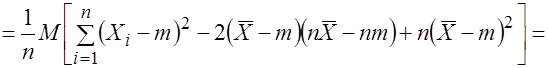
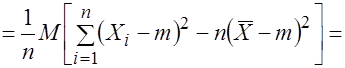
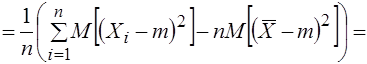
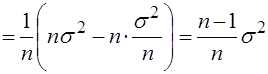Чтобы получить несмещенную оценку дисперсии, оценку (3.14) нужно исправить, то есть домножить на . Тогда получим несмещенную выборочную дисперсию

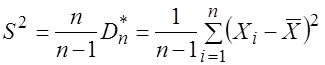. (3.19)

Отметим, что формулы (3.14) и (3.19) отличаются лишь знаменателем, и при больших значениях выборочная и несмещенная дисперсии отличаются мало. Однако при малом объеме выборки следует пользоваться соотношением (3.19).

Для оценки среднего квадратического отклонения случайной величины используют так называемое “исправленное” среднее квадратическое отклонение, которое равно квадратному корню из несмещенной дисперсии: .

< Предыдущая		Следующая >