3.4. Интервальные - оценки

В статистике имеются два подхода к оцениванию неизвестных параметров распределений: точечный и интервальный. В соответствии с точечным оцениванием, которое рассмотрено в предыдущем разделе, указывается лишь точка, около которой находится оцениваемый параметр. Желательно, однако, знать, как далеко может отстоять в действительности этот параметр от возможных реализаций оценок в разных сериях наблюдений.

Ответ на этот вопрос – тоже приближенный – дает другой способ оценивания параметров – интервальный. В соответствии с этим способом оценивания находят интервал, который с вероятностью, близкой к единице, накрывает неизвестное числовое значение параметра.

Понятие интервальной оценки

Точечная оценка является случайной величиной и для возможных реализаций выборки принимает значения лишь приближенно равные истинному значению параметра . Чем меньше разность , тем точнее оценка. Таким образом, положительное число , для которого , характеризует точность оценки и называется Ошибкой оценки (или предельной ошибкой).

Доверительной вероятностью (или надежностью) называется вероятность β, с которой осуществляется неравенство , т. е.

. (3.20)

Заменив неравенство равносильным ему двойным неравенством , или , получим

. (3.21)

Интервал 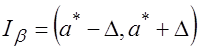, накрывающий с вероятностью β, , неизвестный параметр , называется Доверительным интервалом (или интервальной оценкой), соответствующим доверительной вероятности β.

Случайной величиной является не только оценка , но и ошибка : ее значение зависит от вероятности β и, как правило, от выборки. Поэтому доверительный интервал случаен и выражение (3.21) следует читать так: “Интервал накроет параметр с вероятностью β ”, а не так: “Параметр попадет в интервал с вероятностью β ”.

Смысл доверительного интервала состоит в том, что при многократном повторении выборки объема в относительной доле случаев, равной β, доверительный интервал, соответствующий доверительной вероятности β, накрывает истинное значение оцениваемого параметра. Таким образом, доверительная вероятность β характеризует Надежность доверительного оценивания: чем больше β, тем вероятнее, что реализация доверительного интервала содержит неизвестный параметр.

Следует, однако, иметь в виду, что с ростом доверительной вероятности β в среднем растет длина доверительного интервала, то есть уменьшается точность доверительного оценивания. Выбор доверительной вероятности определяется конкретными условиями; обычно используются значения β, равные 0,90; 0,95; 0,99.

Вероятность (3.22)

называется Уровнем значимости и характеризует относительное число ошибочных заключений в общем числе заключений.

В формуле (3.21) границы доверительного интервала симметричны относительно точечной оценки. Однако не всегда удается построить интервал, обладающий таким свойством. Более общим является следующее определение.

Доверительным интервалом (или Интервальной оценкой) параметра с доверительной вероятностью β, 0< β <1, называется интервал со случайными границами , , накрывающий с вероятностью β неизвестный параметр , т. е.

. (3.23)

Иногда вместо двусторонних доверительных интервалов рассматривают односторонние доверительные интервалы, полагая или .

Построение интервальных оценок

Доверительный интервал задается своими концами и . Однако найти функции и из условия (3.23) невозможно, поскольку закон распределения этих функций зависит от закона распределения ξ и, следовательно, зависит от неизвестного параметра . Используют следующий прием, позволяющий в ряде случаев построить доверительный интервал. Подбирается такая функция , чтобы:

- ее закон распределения был известен и не зависел от неизвестного параметра ;

- функция Была непрерывной и строго монотонной по .

Тогда для любого β можно выбрать два числа и так, чтобы выполнялось равенство

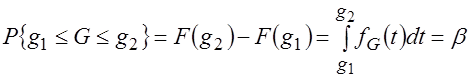. (3.24)

Отсюда находят и как квантили функции распределения . Границы искомого доверительного интервала выражают через найденные квантили и выборочные данные, используя для этого соотношения, связывающие новую и старую случайные величины.

Если плотность распределения случайной величины Симметрична, то доверительный интервал симметричен относительно точечной оценки , и для нахождения границ доверительного интервала вместо условия (3.23) можно использовать соотношение (3.21).

Основные статистические распределения

Построение разного рода оценок и статистических критериев часто основывается на использовании ряда специальных распределений случайных величин.

Нормальное распределение. Случайная величина имеет нормальное распределение с параметрами и , что обозначается как 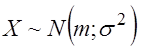, если плотность вероятности этой случайной величины имеет вид

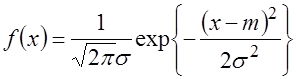. (3 .25)

График плотности вероятности случайной величины, имеющей нормальное распределение, представлен на рисунке 3.5, на котором видно, что максимум функции находится в точке .

Поскольку нормальное распределение подробно изучается в курсе теории вероятностей, напомним свойства нормальной случайной величины, которые будут использоваться в дальнейшем.

Рис. 3.5

1) , .

2) Случайная величина называется Центрированной, если ее математическое ожидание равно нулю. Для того чтобы центрировать случайную величину, надо вычесть из нее математическое ожидание:

.

3) Случайная величина называется Нормированной, если ее дисперсия равна единице, а математическое ожидание равно нулю.

Для того чтобы нормировать случайную величину, надо ее поделить на среднее квадратическое отклонение:

.

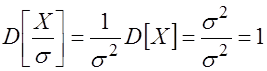Центрированная и нормированная нормальная случайная величина называется стандартной. Таким образом, стандартной будет случайная величина

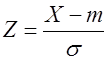~ . (3.26)

Вероятность попадания случайной величины в интервал (α,β) вычисляется по формуле

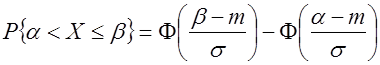, (3.27)

Где 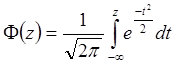- интеграл вероятности, представляющий собой функцию распределения стандартной нормально распределенной случайной величины. Интеграл вероятности табулирован. Его значения приведены в таблице В Приложения.

Для стандартной нормальной случайной величины и симметричного промежутка формула (3.27) принимает следующий вид:

. (3.28)

Распределение (хи-квадрат). Если , независимые стандартные нормальные случайные величины, то говорят, что случайная величина

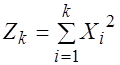(3.29)

Имеет распределение хи-квадрат с степенями свободы, что обозначается как . Графики плотности вероятности для двух значений степени свободы приведены на рис.3.6.

Рис. 3.6

С увеличением числа степеней свободы плотность вероятности стремится к нормальной. При плотность вероятности постоянно убывает, а при имеет единственный максимум , , .

Распределение Стьюдента. Пусть , , , - независимые стандартные нормальные случайные величины. Тогда случайная величина

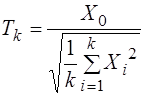(3.30)

Имеет распределение Стьюдента с степенями свободы, что обозначается как , при этом

, .

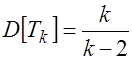На рис.3.7 приведены кривые стандартного нормального распределения (кривая 1) и плотности распределения Стьюдента (кривая 2).

Рис. 3.7

При плотность распределения Стьюдента стремится к плотности стандартной нормальной случайной величины.

На практике, как правило, используется не плотность вероятности, а Квантиль Распределения. Напомним, что квантилью порядка (или уровня) непрерывной случайной величины называется такое ее значение , которое удовлетворяет равенству ,

Где - функция распределения, а - заданное значение вероятности. Рис.3.8 поясняет понятие квантили порядка .

Рис. 3.8

Следующая теорема устанавливает свойства основных выборочных характеристик, вычисленных по выборке, соответствующих нормальному распределению.

Теорема Фишера. Пусть - случайная выборка из генеральной совокупности 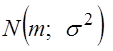, тогда выборочное среднее 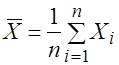и несмещенная выборочная дисперсия 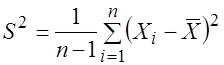независимы, и при этом

1) случайная величина имеет распределение ;

2) случайная величина имеет распределение ;

3) случайная величина имеет распределение .

Доказательство теоремы приведено в [2].

Интервальные оценки математического ожидания нормального распределения

Интервальная оценка математического ожидания при известной дисперсии. Построим доверительный интервал для математического ожидания наблюдаемой случайной величины при известной дисперсии по выборке .

Образуем вспомогательную случайную величину 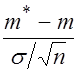, где 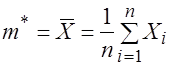- точечная оценка математического ожидания . Согласно утверждению 1 теоремы Фишера, случайная величина имеет нормальное распределение 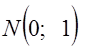и ее функция распределения не зависит от неизвестного параметра.

Доверительный интервал, соответствующий надежности β, определяется из условия (3.20), которое в нашем случае имеет вид

. (3.31)

Неравенства и 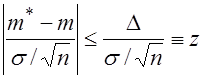являются равносильными, то есть для любой выборки они выполняются или не выполняются одновременно, поэтому соотношение (3.31) можно записать в виде

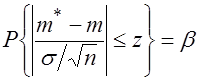. (3.32)

Поскольку случайная величина имеет стандартное нормальное распределение, вероятность в левой части формулы (3.32) можно выразить через нормальную стандартную функцию распределения по формуле (3.7):

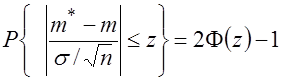. (3.33)

Приравняв правую часть формулы (3.33) заданной доверительной вероятности β, получим уравнение 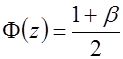. Решение этого уравнения является квантилью порядка 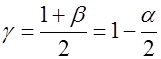стандартного нормального распределения и определяется по таблице значений стандартной нормальной функции распределения (см. табл. В Приложения). Предельная ошибка вычисляется по формуле 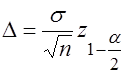. Таким образом, доверительным интервалом математического ожидания, соответствующим надежности β, является интервал

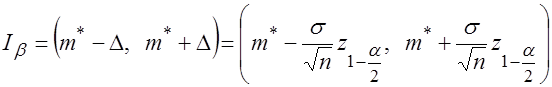. (3.34)

Интервальная оценка математического ожидания при неизвестной дисперсии. По выборке из нормального распределения требуется построить доверительный интервал для неизвестного математического ожидания при неизвестной дисперсии D=σ2.

Введем новую случайную величину 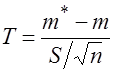, где - несмещенная выборочная дисперсия.

Статистика согласно утверждению 3 теоремы Фишера имеет распределение Стьюдента с степенями свободы. Рассуждая аналогично случаю, когда дисперсия известна, получим следующий доверительный интервал для математического ожидания:

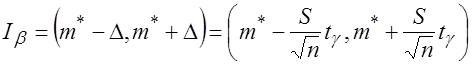, (3.35)

Где - квантиль порядка 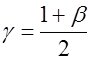распределения Стьюдента. В отличие от доверительного интервала (3.34) длина интервала (3.35) случайна и зависит от случайной величины . Поскольку с увеличением числа степеней свободы распределение Стьюдента быстро приближается к нормальному, то для больших выборок интервалы (3.34) и (3.35) практически совпадают.

Пример 3.2. По результатам 9 измерений напряжения батареи получено среднее арифметическое значение 30,6В. Точность вольтметра характеризуется средним квадратическим отклонением 0,2В. Требуется найти доверительный интервал для истинного значения напряжения батареи, соответствующий доверительной вероятности β=0,95, предполагая, что контролируемый признак имеет нормальный закон распределения.

Решение. Для нахождения доверительного интервала воспользуемся формулой (3.34). Квантиль порядка 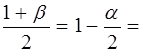0,975 найдем по таблице А Приложения: 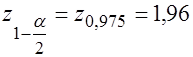.Поскольку предельная ошибка 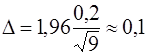, то доверительный интервал имеет вид

.

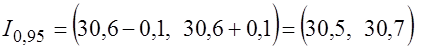Интервальная оценка дисперсии нормального распределения

Построим доверительный интервал для дисперсии D=σ2 наблюдаемой случайной величины ~ по случайной выборке при неизвестном математическом ожидании.

Введем случайную величину (статистику) 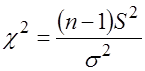, (3.36)

Которая согласно утверждению 2 теоремы Фишера имеет распределение с степенями свободы. Поскольку плотность распределения этого закона асимметрична, доверительный интервал, соответствующий надежности β, найдем из формулы (3.31) в виде:

. (3.37)

Обычно доверительный интервал для случайной величины выбирают так, чтобы вероятность ее попадания за пределы этого интервала влево и вправо была одинаковой ( рис. 3.9):

.

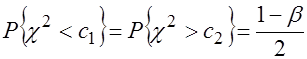Тогда условия для определения значений и будут иметь вид:

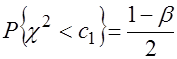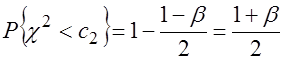, . (3.38)

По таблице квантилей - распределения ( табл. С Приложения) найдем

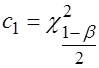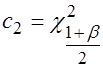, . (3.39)

Рис. 3.9.

Неравенства 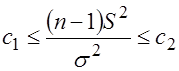эквивалентны неравенствам 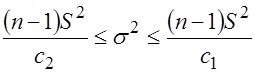, поэтому

.

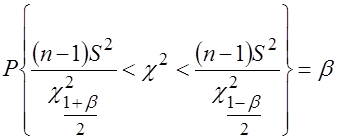Следовательно, интервал

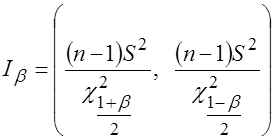(3.40)

Является доверительным интервалом дисперсии, соответствующим доверительной вероятности β.

Пример 3.3. По данным выборочного контроля найти выборочное математическое ожидание и несмещенную оценку дисперсии нормальной случайной величины ξ. Найти доверительные интервалы для них, соответствующие доверительной вероятности β=0,98.

Таблица 3.4

	42	43	45	46	48	51	52	54
	1	2	3	6	4	3	1	1

Решение. Выборочное математическое ожидание найдем по формуле (3.14), используя табл.3.4

При .

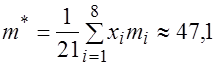Несмещенную выборочную дисперсию вычислим по формуле (3.19):

, .

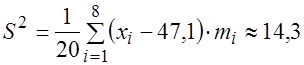Доверительный интервал для математического ожидания определим по формуле (3.35). При из таблицы А Приложения находим квантиль распределения Стьюдента 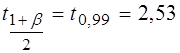. Вычислив предельную ошибку ,

Получим искомый доверительный интервал для математического ожидания:

.

Границы доверительного интервала для дисперсии определим по формуле (3.20). По таблице квантилей распределения χ2 (см. табл. С Приложения) при определим квантили:

, .

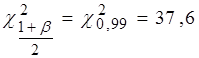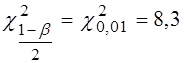Подставив эти значения, а также и в формулу (3.20), получим искомый доверительный интервал для дисперсии

.

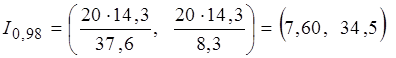Вопросы для самопроверки

2. Что называется выборкой?

3. Как произвести оценку выборочного математического ожидания и выборочной дисперсии?

4. Как найти функцию распределения для дискретной случайной величины?

5. Что такое несмещенная оценка параметра?

6. Дайте определение состоятельной оценки.

7. Что такое интервальная оценка?

< Предыдущая		Следующая >