3.2. Систематизация выборки

Пусть Х1, х 2, … ,х N - реализация случайной выборки.

Вариационным рядом Называется последовательность элементов реализации случайной выборки, расположенных в неубывающем порядке, при этом одинаковые элементы могут повторяться.

Пусть наблюдаемая в эксперименте случайная величина ξ дискретна и принимает различных значений , которые обозначим , , …, .

ПримечанИе: В дальнейшем величины, получаемые из опытных данных, будем обозначать теми же символами, что и теоретические аналоги, со знаком * вверху.

Относительной частотой значения (Или статистической вероятностью события называется случайная величина

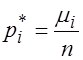, (3.1)

Где μi - частота значения , которое принимает случайная величина ( т. е. число элементов выборки =( ..., ),принявших значение ). Согласно закону больших чисел, сближается с вероятностью при , т. е. относительные частоты можно рассматривать при больших объемах выборки в качестве приближенных значений (оценок) для неизвестных вероятностей .

Статистическим рядом Называется последовательность разных значений случайной величины, расположенных в возрастающем порядке, с указанием значений относительных частот. Статистический ряд, как правило, записывается в виде таблицы (табл.3.1).

Таблица 3.1

Zi	Z1	Z2	Z3	. . .	Zn
P*i	P*1	P*2	P*3	. . .	P*n

Важной характеристикой выборки является эмпирическая функция распределения.

Эмпирической (выборочной) функцией распределения Fn* (X), построенной по случайной выборке, называется относительная частота события { ξ=< X}:

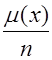, , (3.2)

Где μ(Х) - случайная величина, равная числу тех наблюдений ..., , значения которых не превосходят .

Чтобы получить значение эмпирической функции распределения при данном значении для реализации выборки , надо подсчитать значение μ(Х) для реализации выборки, т. е. просуммировать значения частот тех элементов , которые меньше . Получим

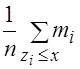. (3.3)

Свойства эмпирической функции распределения аналогичны свойствам обычной функции распределения, а именно:

1) - неубывающая функция по , является ступенчатой со скачками в точках ,

2) для любого , причем полагают, что

, .

Эмпирическая функция распределения является приближенным значением (т. е. оценкой) теоретической функции распределения наблюдаемой случайной величины ξ:

.

Пример 3.1. Проводятся измерения деталей с точностью до одного миллиметра. Оказалось, что отклонения диаметров изготовленных деталей от заданного размера составили следующую выборку объема : 0, -2, -4, 3, 0, 0, -1, 2, -2, -1, 0, -1, 3, 2, 0, -1, -2, 0, -1, 2.

Построить вариационный и статистический ряды, полигон относительных частот, эмпирическую функцию распределения.

Решение. Вариационным рядом заданной выборки будет последовательность: -4, -2, -2, -2, -1, -1, -1, -1, -1, 0, 0, 0, 0, 0, 0, 2, 2, 2, 3, 3.

Статистический ряд представим таблицей (табл.3.2):

Таблица 3.2

	-4	-2	-1	0	2	3

Полигон относительных частот этого распределения изображен на рис.3.2.

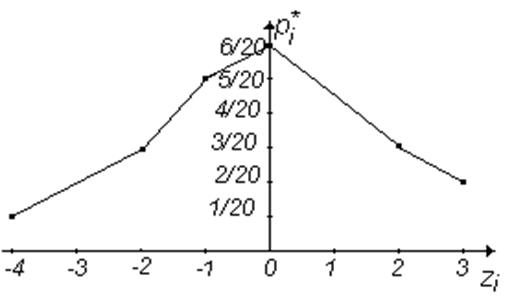
Рис. 3.2

Для полученного статистического ряда вычислим значения эмпирической функции распределения, используя формулу (3.3)

График этой функции представлен на рис. 3.3.

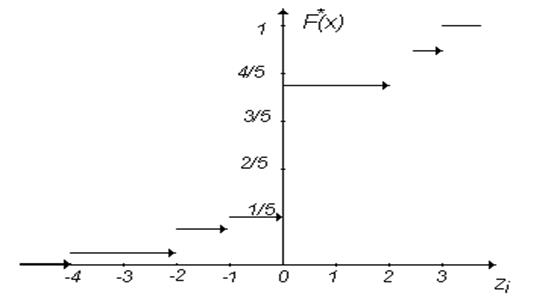
Рис. 3.3.

Гистограмма

Если наблюдаемая случайная величина ξ непрерывна или объем выборки большой, то вариационный и статистический ряды будут трудно обозримыми множествами, практически не будет равных элементов выборки. В этом случае используется процедура группировки выборки, которую рассмотрим для реализации выборки . Интервал возможных значений ξ делят точками на непересекающихся полуинтервалов (разрядов) , . Для каждого разряда подсчитывают частоту - число элементов выборки, попавших в этот разряд. При этом 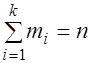. В интервал включают значения, больше или равные нижней границе и меньше верхней границы. Далее находят относительные частоты (статистические вероятности) 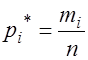. Группированные данные удобно представить в виде интервального статистического ряда – последовательности пар 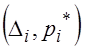, или в виде таблицы (табл. 3.3). Часто группу элементов выборки, входящих в интервал , заменяют средней точкой 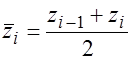. Таблица 3.3

			…
			…

Обычно длина разрядов выбирается одинаковой, т. е. равной 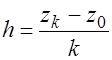. Число разрядов выбирается в зависимости от объема выборки так, чтобы построенный ряд не был громоздким и в то же время позволял выявить характерные особенности изменения случайной величины. Для определения можно рекомендовать формулу Стерджеса

, (3.4)

Которая дает нижнюю оценку величины . В качестве значения следует брать ближайшее целое число.

Группированный статистический ряд наглядно можно изобразить в виде гистограммы. Для ее построения на оси абсцисс откладывают разряды длиною , и на каждом из них, как на основании, строят прямоугольник. В результате получают ступенчатую фигуру, которую называют Гистограммой.

Высота I–го частичного прямоугольника при построении Гистограммы частот равна отношению (плотность частоты).

Площадь I–го частичного прямоугольника численно равна 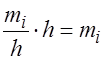, а площадь гистограммы частот численно равна объему выборки, т. е.

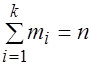, (3.5)

При построении Гистограммы относительных частот:

Высота I–го частичного прямоугольника равна отношению относительной частоты к длине интервала 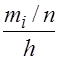(плотность относительной частоты); площадь I–го частичного прямоугольника численно равна 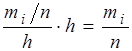; площадь гистограммы относительных частот численно равна

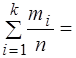1. (3.6)

Гистограмма относительных частот является статистическим аналогом плотности распределения наблюдаемой случайной величины ξ.

Гистограмма изображена на рис. 3.4.

Рис. 3.4

< Предыдущая		Следующая >