2.2.2. Дисперсия случайной величины
Из определения математического ожидания следует, что оно определяет среднее значение случайной величины. Дисперсия характеризует среднюю величину отклонения значений случайной величины от математического ожидания.
Пусть x обозначает дискретную или абсолютно непрерывную случайную величину.
Определение. Моментом второго порядка случайной величины x называется математическое ожидание квадрата этой случайной величины, т. е. число M(x2).
Пусть в формулах (2.18) и (2.19) функция G(X)=X2. Тогда для моментов второго порядка случайной величины x имеют место формулы
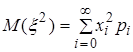 , (2.21)
, (2.21)
![]() . (2.22)
. (2.22)
Величина x-M(x) определяет отклонение случайной величины x От математического ожидания M(x).
Определение. Дисперсией случайной величины x называется момент второго порядка случайной величины (x - M(x)). Дисперсию обозначают D(x). Таким образом, дисперсия случайной величины x определяется формулой
D(x)=M[(x - M(x))2] . (2.23)
Стандартным или средним квадратическим отклонением называют величину, равную квадратному корню из дисперсии и обозначают ![]() :
: ![]() =
=![]() .
.
Из равенств (2.18), (2.19) для моментов второго порядка следуют формулы для вычисления дисперсии дискретной и абсолютно непрерывной случайных величин соответственно
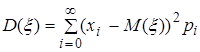 (2.24)
(2.24)
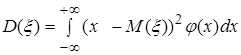 (2.25)
(2.25)
Дисперсия не существует, если ряд (2.24) или несобственный интеграл (2.25) расходятся.
Свойства дисперсии
1. Для любой случайной величины x выполняется неравенство D(x) ≥ 0.
2. При умножении случайной величины x на постоянное число С дисперсия умножается на квадрат этого числа, т. е. справедливо равенство
D(CX)=C2D(x).
3. Справедлива следующая формула для вычисления дисперсии
D(x)=M(x2)- M2(x) , (2.26)
То есть дисперсия случайной величины равна разности второго момента этой величины и квадрата математического ожидания этой же величины.
4. Если случайные величины x и h независимы, дисперсия их алгебраической суммы равна сумме дисперсий, т. е.
D(x+h)=D(x)+D(h). (2.27)
5. Дисперсия постоянной величины С равна нулю.
Пусть x обозначает Дискретную случайную величину с рядом распределения
![]()
![]() Xi X1 X2 , …, Xn…
Xi X1 X2 , …, Xn…
Pi p1 P2 , …, PN… .
В этом случае согласно свойству 3 дисперсия вычисляется по формуле
D(X)=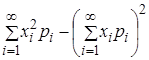 . (2.28)
. (2.28)
| < Предыдущая | Следующая > |
|---|