2.2.3. Нормальное распределение случайной величины

Нормальное распределение часто используется для описания случайных явлений, в которых на результат измерения влияет большое число независимых случайных факторов.

Определение. Случайная величина ξ имеет Нормальное или гауссовское Распределение, Если Ее плотность распределения вероятностей при всех X задается равенством 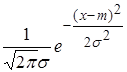. (2.29)

Числа M и σ называются параметрами распределения: параметр M Может быть любым действительным числом: -∞ < M < +∞, а параметр σ – положительным: σ>0. Символическая запись означает, что cлучайная величина ξ имеет нормальное распределение с параметрами M и σ2.

Отметим некоторые свойства графика этой функции (кривой нормального распределения).

Во-первых, функция Принимает максимальное значение при X=M.

Во-вторых, функция симметрична относительно вертикальной прямой X=M.

В-третьих, асимптотой кривой нормального распределения является ось ОХ. Особую роль играет нормальное распределение с параметрами M=0, σ=1, которое часто называют Стандартным (или нормированным) Нормальным распределением. Плотность стандартного нормального распределения имеет вид

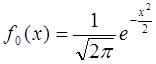, (2.30) Ниже приведен график Y = F0(X).

Функция распределения случайной величины, имеющей нормальный закон, может быть представлена в виде несобственного интеграла

F(X) =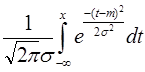. (2.31)

Функцию распределения стандартного Нормального закона

Ф(Х) = 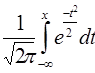(2.32)

Часто называют функцией Лапласа, для которой имеются таблицы значений, широко используемые в статистических исследованиях. Рассмотрим свойства нормального распределения.

Свойство 1. Пусть случайная величина ξ имеет нормальное распределение с параметрами M и σ, т. е. . Тогда математическое ожидание равно параметру M, А дисперсия равна σ2 , Т. е.

M(ξ)=M; D(ξ)= σ2.

Свойство 2. Между функциями распределения F(X) и Имеет место следующее соотношение

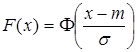. (2.33)

Таблицы значений функции Не содержат значений при X<0. В таких случаях можно использовать следующее свойство.

Свойство 3. При любых значениях X имеет место равенство

. (2.34)

Следующее свойство позволяет вычислить вероятность попадания случайной величины в интервал, используя таблицы значений функции .

Свойство 4. Пусть случайная величина ξ имеет нормальное распределение с параметрами M и σ, Т. е. . Тогда вероятность попадания случайной величины ξ в интервал [A,B] можно найти по формуле

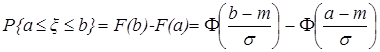. (2.35)

В частности, для симметричного интервала относительно M имеет место формула для любого :

. (2.36)

Формула (2.36) непосредственно следует из (2.35), в которой надо положить и использовать свойство, что . Тогда получим

.

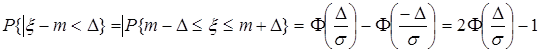Свойство 5 (закон трех сигм). Пусть случайная величина ξ имеет нормальное распределение с параметрами M и σ, т. е. . Тогда с вероятностью больше 0,99 значения случайной величины содержатся в интервале

Действительно, по свойству 4, . Из таблицы функций находим значение =0,9987. Отсюда следует, что

< Предыдущая		Следующая >