8.3. Задачи для самостоятельного решения

8.15. Случайная величина Х имеет плотность

Найти математическое ожидание и дисперсию Х.

Ответ: М(Х) = 0,5909; D(Х) = 0,0781.

8.16. Случайная величина Х имеет плотность

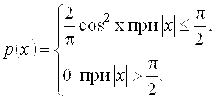
Найти математическое ожидание и дисперсию Х.

Ответ: .

8.17. Случайная величина Х задана плотностью распределения

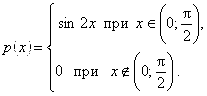
Найти математическое ожидание функции (не находя предварительно плотности распределения ).

Ответ: .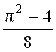

8.18. Плотность случайной величины Х имеет вид

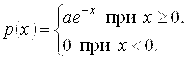
Найти коэффициент А. Вычислить моду, медиану, математическое ожидание, дисперсию, начальные и центральные моменты первого, второго и третьего порядков случайной величины Х.

Ответ: ,

8.19. Случайная величина Х задана плотностью распределения

Найти начальные моменты случайной величины Х.

Ответ: Не существуют при K ³ 6.

8.20. Плотность вероятности случайной величины Х имеет вид

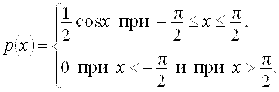
Найти математическое ожидание и дисперсию случайной величины

Ответ:

8.21. Случайная величина Х имеет функцию распределения

Найти математическое ожидание случайной величины .

Ответ:

8.22. По данным задачи 8.9 (при ) найти моду и медиану распределения; вероятность того, что случайная величина Х окажется в промежутке математическое ожидание и дисперсию Х.

Ответ: .

8.23. Найти математическое ожидание и дисперсию случайной величины, плотность вероятности которой имеет вид

(распределение Лапласа).

Ответ:

8.24. Случайная величина Х подчинена закону Симпсона («закону равнобедренного треугольника») на участке от –А до +А (рис. 8.10). Написать выражение плотности распределения; построить график функции распределения; найти числовые характеристики случайной величины Х: , , , . Найти вероятность попадания случайной величины Х в интервал .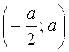

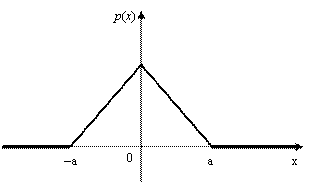Рис. 8.10

Ответ:

.

8.25. Случайная величина Х подчинена закону распределения с плотностью, которая задана формулой

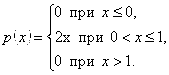
Найти коэффициент асимметрии распределения.

Ответ: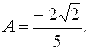

8.26. Найти коэффициент асимметрии и эксцесс случайной величины, распределнной по закону Лапласа с плотностью

Ответ: ;

8.27. Случайная величина Х, сосредоточенная на интервале , задана функцией распределения . Найти моду и медиану случайной величины Х.

Ответ: ;

8.28. Найти значения для случайной величины Х, функция распределения которой

Ответ:

8.29. Кривая распределения случайной величины Х представляет собой полуэллипс с полуосями А и B. Полуось А известна. Определить B. Найти и функцию распределения .

Ответ: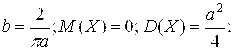

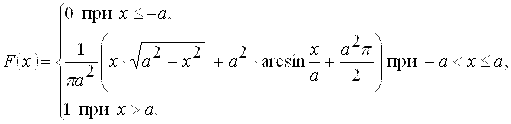
8.30. СЛучайная величина Х задана плотностью распределения

Найти коэффициент асимметрии и эксцесс.

Ответ: ;

< Предыдущая		Следующая >