8.4. Равномерный закон распределения
Непрерывная случайная величина Х имеет Равномерный закон распределения на отрезке ![]() , если ее плотность вероятности Р(Х) постоянна на этом отрезке и равна нулю вне его, т. е.
, если ее плотность вероятности Р(Х) постоянна на этом отрезке и равна нулю вне его, т. е.

Функция распределения случайной величины Х, распределенной по равномерному закону, есть

Математическое ожидание ![]() дисперсия
дисперсия 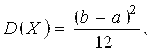 а среднее квадратическое отклонение
а среднее квадратическое отклонение  .
.
Пример 8.14. Поезда метрополитена идут регулярно с интервалом 3 мин. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придется не больше минуты. Найти математическое ожидание и среднее квадратическое отклонение случайной величины Х — времени ожидания поезда.
Решение. Случайная величина Х — время ожидания поезда на временном (в минутах) отрезке ![]() имеет равномерный закон распределения
имеет равномерный закон распределения ![]() . Поэтому вероятность того, что пассажиру придется ждать не более минуты, равна
. Поэтому вероятность того, что пассажиру придется ждать не более минуты, равна ![]() От равной единице площади прямоугольника (рис. 8.11), т. е.
От равной единице площади прямоугольника (рис. 8.11), т. е.
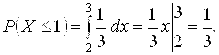
![]() Мин,
Мин, ![]()
![]() мин.
мин.
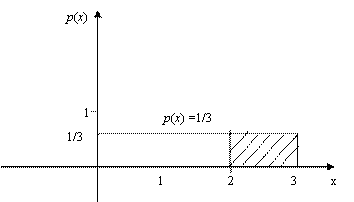 |
Рис. 8.11
Пример 8.15. Найти математическое ожидание и дисперсию произведения двух независимых случайных величин ξ и η с равномерными законами распределения: ξ в интервале ![]() , η — в интервале
, η — в интервале ![]() .
.
Решение. Так как математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий, то ![]() . Для нахождения дисперсии воспользуемся формулой
. Для нахождения дисперсии воспользуемся формулой
![]()
![]() найдем по формуле
найдем по формуле
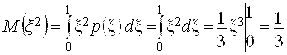 .
.
Аналогично рассчитаем
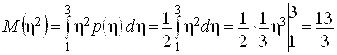 .
.
Следовательно,
![]() .
.
Пример 8.16. Вычислить математическое ожидание и дисперсию определителя
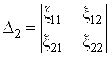 ,
,
Элементы которого ![]() — независимые случайные величины с
— независимые случайные величины с ![]() и
и ![]()
Решение. Вычислим математическое ожидание
![]()
Для нахождения дисперсии![]() докажем, что если ξ и η — независимые случайные величины, то
докажем, что если ξ и η — независимые случайные величины, то ![]()
Действительно,

Следовательно,
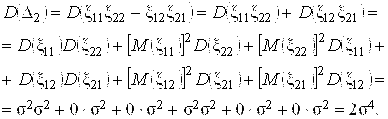
Замечание. Для определителя N-го порядка ![]() ;
; ![]()
Пример 8.17. Автоматический светофор работает в двух режимах: 1 мин. горит зеленый свет и 0,5 мин — красный и т. д. Водитель подъезжает к перекрестку в случайный момент времени. 1. Найти вероятность того, что он проедет перекресток без остановки. 2. Составить закон распределения и вычислить числовые характеристики времени ожидания у перекрестка.
Решение. 1. Момент проезда автомобиля T через перекресток распределен равномерно в интервале, равном периоду смены цветов светофора. Этот период равен 1 + 0,5 = 1,5 мин. Для того чтобы машина проехала через перекресток не останавливаясь, достаточно того, чтобы момент проезда пришелся на интервал времени ![]() . Тогда
. Тогда
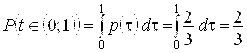 .
.
2. Время ожидания ![]() является смешанной случайной величиной: с вероятностью
является смешанной случайной величиной: с вероятностью ![]() она равна нулю, а с вероятностью
она равна нулю, а с вероятностью ![]() принимает с равномерной плотностью вероятностей любые значения между 0 и 0,5 мин; тогда график функции распределения случайной величины
принимает с равномерной плотностью вероятностей любые значения между 0 и 0,5 мин; тогда график функции распределения случайной величины ![]() имеет вид, изображенный на рис. 8.12:
имеет вид, изображенный на рис. 8.12:
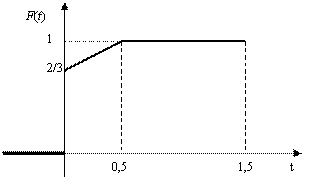 |
Рис. 8.12
То есть ![]() при
при ![]() ;
; 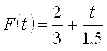 при
при ![]() ;
; ![]() при
при ![]() .
.
Среднее время ожидания у перекрестка
 Мин.
Мин.
Дисперсия времени ожидания
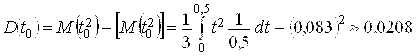 Мин2;
Мин2;
![]() Мин.
Мин.
| < Предыдущая | Следующая > |
|---|