8.2. Числовые характеристики непрерывных случайных величин
Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством

Где Р(Х) — плотность распределения случайной величины Х. Предполагается, что интеграл сходится абсолютно. В частности, если все возможные значения принадлежат интервалу ![]() , то
, то 
Дисперсия непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох определяется равенством

Если интеграл сходится, или равносильным равенством

В частности, если все возможные значения Х принадлежат интервалу ![]() , то
, то

Или

Все свойства математического ожидания и дисперсии для дискретных случайных величин справедливы и для непрерывных величин.
Среднее квадратическое отклонение непрерывной случайной величины определяется равенством
![]() .
.
Модой ![]() непрерывной случайной величины Х называется ее наиболее вероятное значение (для которого плотность вероятности Р(Х) достигает максимума).
непрерывной случайной величины Х называется ее наиболее вероятное значение (для которого плотность вероятности Р(Х) достигает максимума).
Медианой ![]() непрерывной случайной величины Х называется такое ее значение, для которого
непрерывной случайной величины Х называется такое ее значение, для которого
![]() .
.
Вертикальная прямая ![]() , проходящая через точку с абсциссой, равной
, проходящая через точку с абсциссой, равной ![]() , геометрически делит площадь фигуры под кривой распределения на две равные части (рис. 8.7).
, геометрически делит площадь фигуры под кривой распределения на две равные части (рис. 8.7).
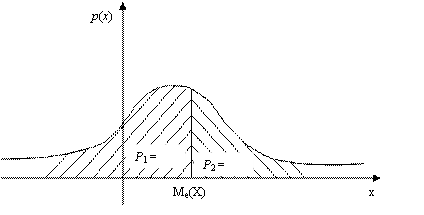 |
Рис. 8.7
Очевидно, что ![]() .
.
Начальный теоретический момент порядка k непрерывной случайной величины Х определяется равенством
 .
.
Центральный теоретический момент порядка K непрерывной случайной величины Х определяется равенством
 .
.
Если все возможные значения Х принадлежат интервалу ![]() , то
, то
 ,
, 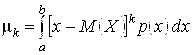 .
.
Очевидно, что ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Центральные моменты выражаются через начальные моменты по формулам:
. Центральные моменты выражаются через начальные моменты по формулам:
![]() ,
,
![]() ,
,
![]() .
.
Математическое ожидание М(Х), или первый начальный момент, характеризует среднее значение распределения случайной величины Х; второй центральный момент, или дисперсия ![]() , — степень рассеяния распределения Х относительно М(Х).
, — степень рассеяния распределения Х относительно М(Х).
Третий центральный момент служит для характеристики асимметрии распределения.
Величина ![]() называется Коэффициентом асимметрии случайной величины.
называется Коэффициентом асимметрии случайной величины.
А = 0, если распределение симметрично относительно математического ожидания.
Четвертый центральный момент характеризует крутость распределения.
Эксцессом случайной величины называется число
![]() .
.
Кривые более островершинные, чем кривая для нормального распределения, обладают положительным эксцессом, более плосковершинные — отрицательным эксцессом.
Пример 8.7. Дана функция
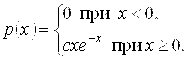
При каком значении параметра С эта функция является плотностью распределения некоторой непрерывной случайной величины Х? Найти математическое ожидание и дисперсию случайной величины Х.
Решение. Для того чтобы Р(Х) была плотностью вероятности некоторой случайной величины Х, она должна быть неотрицательна, т. е. ![]() , откуда
, откуда ![]() и она должна удовлетворять свойству 4 плотности вероятности.
и она должна удовлетворять свойству 4 плотности вероятности.
Следовательно,
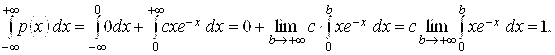
Откуда
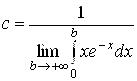 .
.
Найдем интеграл 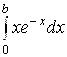 , применив метод интегрирования по частям
, применив метод интегрирования по частям

Таким образом,

И плотность распределения имеет вид
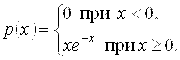
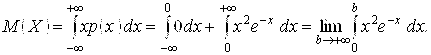

Следовательно,
![]()
Дисперсия ![]()
Вначале найдем

Теперь ![]()
 |
Пример 8.8. Случайная величина Х распределена по «закону прямоугольного треугольника» в интервале
1. Написать выражение плотности распределения.
2. Найти функцию распределения F(Х).
3. Найти вероятность попадания случайной величины Х на участок от ![]() до А.
до А.
4. Найти характеристики величины Х: М(Х), D(Х), ![]() ,
, ![]() .
.
Решение. Так как площадь прямоугольного треугольника есть площадь фигуры, ограниченной кривой распределения и осью абсцисс, то она равна единице: ![]() И, следовательно,
И, следовательно, ![]() . Уравнение прямой АВ в отрезках имеет вид
. Уравнение прямой АВ в отрезках имеет вид 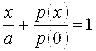 , откуда
, откуда ![]()
 , то есть функция плотности распределения имеет вид
, то есть функция плотности распределения имеет вид
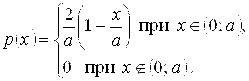
Найдем функцию распределения F(Х):
Если ![]() , то
, то 
Если ![]() , то
, то 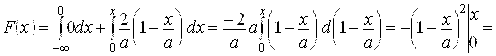

Если ![]() , то
, то 
Таким образом,

Вероятность попадания случайной величины Х на участок от ![]() До А определяется по формуле
До А определяется по формуле
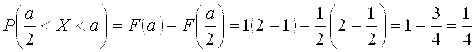 .
.
Найдем математическое ожидание:


Следовательно,
 ,
,
![]() .
.
Так как ![]() , а
, а ![]() ,
, 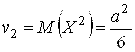 ,
,
 ,
,
То ![]() .
.
Пример 8.9. По данным задачи 8.5 найти математическое ожидание М(Х), дисперсию D(Х), моду М0(Х) и медиану Ме(Х).
Решение. Так как 
То 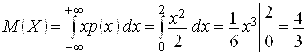 .
.
Дисперсия ![]()
Вначале найдем
 .
.
Следовательно,

График плотности вероятности Р(Х) имеет вид (рис. 8.9)
 |
Рис. 8.9
Плотность вероятности р(Х) максимальна при х = 2, это означает, что М0(Х) = 2.
Из условия ![]() Найдем медиану Ме(Х):
Найдем медиану Ме(Х):  ; откуда
; откуда ![]()
Пример 8.10. Дана функция

Найти коэффициент асимметрии и эксцесс случайной величины Х.
Решение. Плотность распределения случайной величины Х равна
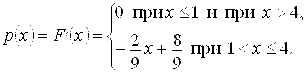
Так как асимметрия ![]() , эксцесс
, эксцесс ![]() , то найдем начальные моменты первого, второго, третьего и четвертого порядков:
, то найдем начальные моменты первого, второго, третьего и четвертого порядков:




Тогда
![]()
![]()
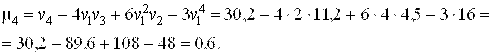
Так как ![]() то
то ![]()
![]()
![]() Следовательно,
Следовательно,
![]()
![]()
Пример 8.11. Плотность случайной величины Х задана следующим образом:

Найти моду, медиану и математическое ожидание Х.
Решение. Найдем математическое ожидание Х:
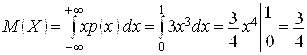 .
.
Так как плотность распределения достигает максимума при Х = 1, то М0(Х) =1. Медиану Ме(Х) найдем из условия ![]() . Для этого вначале найдем функцию распределения
. Для этого вначале найдем функцию распределения ![]() :
:
Если ![]() , то
, то 
Если ![]() , то
, то 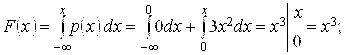
Если ![]() , то
, то 
Таким образом,

Уравнение ![]() равносильно уравнению
равносильно уравнению ![]() , откуда
, откуда  .
.
Пример 8.12. Случайная величина Х задана плотностью распределения

Найти математическое ожидание функции ![]() (не находя предварительно плотности распределения
(не находя предварительно плотности распределения ![]() ).
).
Решение. Воспользовавшись формулой для вычисления математического ожидания функции![]() от случайного аргумента Х
от случайного аргумента Х

Где А и B — концы интервала, в котором заключены возможные значения Х, получим
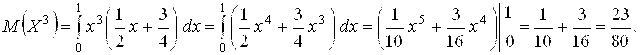
Пример 8.13. Случайная величина Х задана плотностью распределения
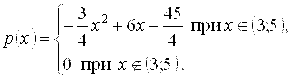
Найти моду, математическое ожидание и медиану величины Х.
Решение. Так как ![]() , то отсюда видно, что при Х = 4 плотность распределения достигает максимума и, следовательно, М0(Х) = 4 (можно было найти максимум методами дифференциального исчисления).
, то отсюда видно, что при Х = 4 плотность распределения достигает максимума и, следовательно, М0(Х) = 4 (можно было найти максимум методами дифференциального исчисления).
Кривая распределения симметрична относительно прямой Х = 4, поэтому М(Х) = Ме(Х) = 4.
| < Предыдущая | Следующая > |
|---|