4. Системы дифференциальных уравнений. 4.1. Основные понятия

Система дифференциальных уравнений первого порядка, разрешенная относительно первых производных искомых функций , и имеющая следующий вид:

Называется Нормальной системой уравнений.

Решением системы называется система непрерывно дифференцируемых на интервале функций , обращающих все уравнения нормальной системы в тождества относительно . В дальнейшем, решение системы часто будет записываться в виде вектор-функции скалярного аргумента, так что ,

Дифференциальное уравнение порядка всегда можно свести к нормальной системе. Обратно, системы дифференциальных уравнений в большинстве случаев сводятся к дифференциальным уравнениям порядка . Решая такое уравнение, можно найти и решение исходной системы дифференциальных уравнений.

Определение. Задачей Коши для системы нормальных дифференциальных уравнений называют задачу об отыскании частного решения этой системы, удовлетворяющего заданным начальным условиям .

Приведем без доказательства теорему, в которой формулируются условия существования и единственности решения задачи Коши для нормальной системы уравнений.

Теорема Коши (о существовании и единственности решения задачи Коши для нормальной системы уравнений).

Пусть правые части Нормальной системы дифференциальных уравнений определены в - мерной области Изменения переменных .

Если в окрестности точки функции Непрерывны и имеют непрерывные частные производные по переменным , то в некотором интервале существует и притом единственное решение этой системы, удовлетворяющее начальным условиям, называемое решением задачи Коши.

Как и любое дифференциальное уравнение, система дифференциальных уравнений имеет бесконечно много решений. Для того чтобы в компактной форме задать множество решений нормальной системы из дифференциальных уравнений обычно используют произвольных постоянных .

Определение. Общим решением нормальной системы Дифференциальных уравнений называют систему функций

Зависящих от Произвольных постоянных, если:

1) При любых допустимых значениях произвольных постоянных функции являются решениями системы уравнений, которые коротко называют частными решениями системы;

2) Любое решение задачи Коши может быть представлено в виде при некоторых значениях произвольных постоянных .

Пример. Свести нормальную систему дифференциальных уравнений

Где Есть неизвестные функции, к уравнению второго порядка от одной неизвестной функции и найти общее решение исходной системы.

Выразим из первого уравнения: . Отсюда найдем производную . Подставив значения и во второе уравнение системы, получим однородное уравнение второго порядка с постоянными коэффициентами . Общее решение этого уравнения имеет вид .

Отсюда, используя равенство , найдем

.

Таким образом, при любых постоянных И система функций

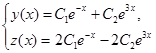
Является решением исходной системы.

Правые части данной системы имеют вид , и определены во всем пространстве . Все частные производные по переменным и : ,,, также существуют и непрерывны во всем пространстве .

В силу теоремы Коши, данная система уравнений имеет единственное решение при любых начальных условиях . Подставив значения в общее решение системы дифференциальных уравнений, получим систему алгебраических уравнений для определения частных значений произвольных постоянныхИВ следующем виде:

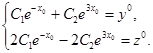
Определитель этой системы равен и отличен от нуля при любом значении .

Следовательно, при любых значениях и произвольные постоянные И находятся однозначно. Это означает, что из полученного общего решения можно найти любое решение задачи Коши для данной системы дифференциальных уравнений.

< Предыдущая		Следующая >