4.2. Линейные неоднородные системы дифференциальных уравнений (ЛНСДУ)

В матричной форме система неоднородных дифференциальных уравнений имеет вид

,

Где – квадратная функциональная матрица коэффициентов системы дифференциальных уравнений, – функциональный вектор-столбец неизвестных, – вектор-столбец производных неизвестных системы уравнений – вектор-столбец правых частей.

Систему называют Соответствующей данной ЛНСДУ однородной системой. Для ЛНСДУ с постоянными коэффициентами справедлива следующая теорема.

Теорема (о структуре общего решения ЛНСДУ).

Общее решение ЛНСДУ Порядка с постоянными коэффициентами и непрерывной на некотором интервале правой частью Равно сумме общего решения соответствующей однородной системы и любого частного решения неоднородной системы дифференциальных уравнений, т. е.

.

Доказательство теоремы аналогично доказательству соответствующей теоремы для дифференциальных уравнений порядка .

Если известна фундаментальная система решений соответствующей однородной системы дифференциальных уравнений и, следовательно, ее общее решение , то для определения частного решения неоднородной системы порядка с постоянными коэффициентами можно воспользоваться Методом вариации произвольных постоянных Лагранжа.

Этот метод заключается в том, что решение ЛНСДУ ищут в виде

,

Т. е. в виде линейной комбинации неизвестных функций и заранее вычисленных фундаментальных решений соответствующей ЛОСДУ.

Предварительно находят производные из системы алгебраических уравнений следующего вида: .

Определителем этой системы является Вронскиан , который не равен нулю при любом , поскольку вектор-решения образуют фундаментальную систему решений соответствующей однородной системы.

При условии данная система линейных неоднородных алгебраических уравнений имеет единственное решение относительно неизвестных , которое представим в виде равенств .

Интегрируя каждое из полученных равенств, получим набор первообразных для функций . Окончательно, получаем функцию

,

Которая, как доказано в общей теории, является частным решением ЛСНДУ при условии непрерывности на некотором интервале вектор-функции .

Для систем неоднородных уравнений с постоянными коэффициентами справедлива теорема о наложении решений, которая доказывается на основании линейных свойств матриц и определений общего решения соответствующей ЛОСДУ и частного решения ЛНСДУ.

Рассмотрим на примере ЛНСДУ второго порядка, как находится его общее решение с использованием метода Лагранжа для отыскания частного решения.

Пример. Решить задачу Коши для ЛНСДУ второго порядка с постоянными коэффициентами.

Характеристическое уравнение соответствующей однородной системы имеет вещественные корни и . Компоненты собственного вектора , соответствующего корню находим из системы 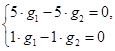в виде

. Соответственно, компоненты собственного вектора , соответствующего корню находим из системы в виде .

Отсюда получаем фундаментальную систему решений соответствующей однородной системы уравнений , и ее общее решение

.

Заменим в общем решении Постоянные Неизвестными функциями И в соответствии с методом неопределенных коэффициентов будем искать частное решение ЛНСДУ в виде .

Предварительно для ЛНСДУ второго порядка решается система уравнений

Линейная относительно производных неизвестных функций .

Для данной системы дифференциальных уравнений указанная система имеет вид

Определителем этой системы является Вронскиан который всегда отличен от нуля, что позволяет найти неизвестные по формулам Крамера

, .

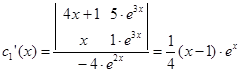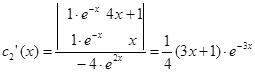Интегрируя полученные дифференциальные уравнения и выделяя первообразные их правых частей , , находим неизвестные функции в виде , . Отсюда, частное решение данной неоднородной системы дифференциальных уравнений НЛДУ равно

.

Окончательно, общее решение данной системы записывается в виде

.

Используя начальные условия, получаем систему для определения постоянных

Отсюда .

Таким образом, решением задачи Коши будет следующее частное решение

.

< Предыдущая		Следующая >