4.2. Линейные однородные системы дифференциальных уравнений

Линейные однородные системы дифференциальных уравнений (ЛОСДУ) имеют самостоятельное значение, а также – вспомогательное значение в качестве первого этапа в процессе решения линейных неоднородных систем дифференциальных уравнений (ЛНСДУ) .

Нормальная ЛОСДУ порядка имеет следующий вид:

В матричной форме эта система имеет вид , где – квадратная функциональная матрица коэффициентов – функциональный вектор-столбец неизвестных, – функциональный вектор-столбец производных неизвестных системы уравнений.

Теорема (о линейных свойствах решений ЛОСДУ).

Если вектор-функции , заданные на некотором интервале , являются решениями линейной однородной системы дифференциальных уравнений, то их линейная комбинация Также является решением.

Теорема доказывается непосредственно на основе линейных свойств матриц.

Определение. Система решений ЛОСДУ, заданных на некотором интервале , называется фундаментальной, если эти решения линейно независимы на интервале , а число этих решений равно порядку системы.

Теорема (критерий фундаментальности решений ЛОСДУ).

Для того чтобы система решений ЛОСДУ порядка с непрерывной на некотором интервале матрицей коэффициентов Была фундаментальной, необходимо и достаточно, чтобы Вронскиан системы был отличен от нуля во всех точках интервала .

Доказательство. Докажем достаточность условия теоремы. Вронскиан системы имеет вид . Признак независимости функций справедлив для вектор-функций и доказывается по аналогичной схеме. Если у системы решений ЛОСДУ порядка , заданных на некотором интервале , Вронскиан не равен нулю во всех точках интервала , то по признаку независимости вектор-функций данная система решений является фундаментальной, что и доказывает достаточность условия теоремы.

Для доказательства необходимости условия теоремы, предположим обратное. Положим, что существует точка , где Вронскиан равен нулю, а система решений ЛОСДУ порядка Является линейно независимой.

Выберем числа , не все равные нулю, и такие, что они являются решениями однородной линейной системы уравнений .

Это возможно по теореме о существовании нетривиального решения, так как определителем этой системы является Вронскиан , который по предположению равен нулю. Линейная комбинация решений Также является решением. Из вида построенной системы следует, что числа Есть коэффициенты решения задачи Коши с начальными условиями вида .

Но таким же начальным условиям удовлетворяет и нулевое решение . Так как по условию доказываемой теоремы матрица коэффициентов непрерывна на интервале , то справедлива теорема о существовании и единственности решения на интервале . Отсюда следует, что построенное решение и нулевое решение совпадают, т. е. , причем не все числа Одновременно равны нулю. Это означает, что решения линейно зависимы, хотя предполагалось обратное. Полученное противоречие завершает доказательство необходимости условия теоремы. Таким образом, теорема полностью доказана.

Теорема (о структуре общего решения ЛОСДУ).

Если ЛОСДУ порядка с непрерывной на некотором интервале матрицей коэффициентов имеет фундаментальную систему из решений, то линейная комбинация произвольных постоянных И Решений , является общим решением ЛОСДУ.

Доказательство теоремы проводится по схеме аналогичной доказательству теоремы о структуре общего решения ЛОДУ порядка .

Если начальные значения Удовлетворяют условиям теоремы Коши, то функция Является единственным решением задачи Коши.

Частным случаем линейных систем однородных дифференциальных уравнений являются ЛОСДУ порядка С числовыми коэффициентами , где – некоторая квадратная числовая матрица коэффициентов.

Так как элементы матрицы являются постоянными функциями, которые непрерывны на любом промежутке, то по теореме о структуре общего решения ЛОСДУ для того, чтобы найти общее решение данной системы уравнений достаточно построить фундаментальную систему решений .

Как было предложено Л. Эйлером, будем искать решение ЛОСДУ с постоянными коэффициентами в виде произведения - мерного вектора на экспоненциальную функцию , где – некоторое число. Дифференцируя эту вектор-функцию и подставляя полученные функции в решаемое дифференциальное уравнение, получим . Так как экспоненциальная функция строго положительна, то справедливо матричное уравнение , которое позволяет найти собственные числа и собственные векторы матрицы коэффициентов.

Одним из методов вычисления собственных чисел матриц является решение уравнения , которое следует из теоремы существования ненулевого решения линейной однородной алгебраической системы уравнений. Раскрывая определитель, получаем алгебраическое уравнение порядка относительно переменной . В теории дифференциальных уравнений данное уравнение называют Характеристическим уравнением ЛОСДУ. Для каждого собственного числа из матричного уравнения находят некоторый собственный вектор . По построению вектор-функция является одним из решений исходного ЛОСДУ.

Из основной теоремы алгебры следует, что характеристическое уравнение ЛОСДУ имеет корней с учетом их кратности. Рассмотрим следующие варианты.

1. Все корней вещественные и различные.

Доказано, что в этом случае ЛОСДУ с постоянными коэффициентами порядка имеет фундаментальных решений вида , где собственные числа и собственные векторы , вычисляются по указанной выше схеме. Соответственно, общее решение ЛОСДУ с постоянными коэффициентами порядка принимает вид .

Пример. Решить ОЛДУ второго порядка .

Характеристическое уравнение данного ОЛДУ имеет вид . Оно имеет вещественные различные корни , . Каждому корню Соответствуют частные решения , , которые образуют фундаментальную систему решений.

Отсюда, есть общее решение ОЛДУ.

Доказано, что ОЛДУ с постоянными коэффициентами порядка в том случае, когда все корни характеристического уравнения вещественные и различные, имеет общее решение аналогичного вида .

2. Все корней вещественные, но среди них есть кратные.

Если некоторый корень имеет кратность , то соответствующее этому корню решение системы ищется в виде вектор-функции , где компоненты вектор-функции Представляют собой полиномы степени с неизвестными коэффициентами. Коэффициенты этих полиномов определяются из системы линейных уравнений, получающейся приравниванием коэффициентов при одинаковых степенях В результате подстановки вектора в исходную систему. Рассмотрим вначале пример ЛОСДУ с постоянными коэффициентами второго порядка, которое имеет один корень кратности два.

Пример. Найти общее решение ЛОСДУ второго порядка

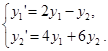
Характеристическое уравнение имеет корень кратности . Поэтому ищем решение системы в виде .

Подставляем это выражение в исходную систему и сокращаем на :

.

Приравнивая коэффициенты при одинаковых степенях , получаем систему линейных алгебраических уравнений относительно неизвестных коэффициентов :

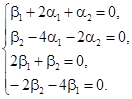
Положим И , где И – произвольные постоянные. Тогда из системы уравнений находим И .

Таким образом, общее решение данной системы имеет вид

.

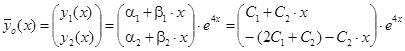Где У. Из теоремы о структуре общего решения ОЛДУ следует, что линейная комбинация Является общим решением ОЛДУ второго порядка с постоянными коэффициентами.

Если ЛОСДУ с постоянными коэффициентами порядка Имеет и простые корни, и кратные корни, то его общее решение находят комбинируя первый и второй способ решения.

3. Среди корней могут быть как вещественные, так и комплексные корни.

Если характеристическое уравнение имеет вещественные коэффициенты, то, как было доказано ранее в теории алгебраических уравнений, каждому комплексному корню обязательно соответствует сопряженный корень .

Рассмотрим вначале ЛОСДУ с постоянными вещественными коэффициентами второго порядка. Если характеристическое уравнение содержит комплексный корень вида , то второй корень обязательно имеет вид . Частными решениями такого ЛОСДУ являются вектор-функции , . Собственные векторы и , вычисляются по стандартной схеме и, как правило, имеют компоненты из комплексных чисел.

Так как исходное ЛОСДУ имеет вещественные коэффициенты, то полезно наряду с решениями, представленными в комплексной форме, иметь вещественные решения.

Для этого, пользуясь формулами Эйлера, выделяют в одном из комплексных решений вещественную и мнимую части решения. Для ЛОСДУ с вещественными коэффициентами вещественная и мнимая части решения также являются решениями, что позволяет получить пару частных вещественных решений, соответствующих данной паре комплексно-сопряженных корней характеристического уравнения.

Пример. Найти общее решение ЛОСДУ второго порядка

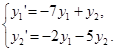
Характеристическое уравнение имеет пару комплексно-сопряженных корней и . Будем искать компоненты собственного вектора , соответствующего корню :

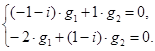
Решение этой системы двух линейных алгебраических уравнений с комплексными коэффициентами находится либо методом исключения неизвестных, либо по формулам Крамера и имеет вид . Отсюда комплексное решение, соответствующее первому комплексному корню получаем в следующем виде:

Пользуясь формулами Эйлера, выделим в решении вещественную и мнимую части:

.

Вещественная и мнимая части решения ,

Образуют фундаментальную систему. Отсюда, общее решение исходной системы имеет вид

.

Доказано, что общее решение ЛОСДУ порядка с постоянными вещественными коэффициентами в общем случае представляет собой линейную комбинацию произвольных постоянных И фундаментальных решений всех указанных выше видов.

< Предыдущая