3.5. Линейные неоднородные дифференциальные уравнения

Рассмотрим линейное неоднородное дифференциальное уравнение (ЛНДУ) порядка

Или коротко , где .

Уравнение , левая часть которого совпадает с левой частью ЛНДУ, называют Соответствующим данному ЛНДУ однородным уравнением.

Теорема (о структуре общего решения ЛНДУ).

Общее решение ЛНДУ Порядка с непрерывными на некотором интервале коэффициентами равно сумме общего решения соответствующего однородного уравнения и любого частного решения ЛНДУ, т. е. .

Доказательство. В первую очередь, подставим функцию В исходное уравнение и убедимся в том, что она действительно является решением ЛНДУ:

При выводе были использованы линейные свойства линейного дифференциального оператора и то, что функция Есть общее решение ОЛДУ, так что , а функция Есть частное решение НЛДУ, так что .

Далее, чтобы доказать, что данное решение является общим, необходимо для заданных начальных условий найти единственную комбинацию Произвольных постоянных, обеспечивающих решение задачи Коши.

Дифференцируя функцию Раз, и подставляя в нее и во все ее производные заданные начальные условия, получим систему линейных уравнений относительно произвольных постоянных следующего вида:

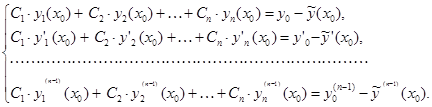
Определителем этой системы является Вронскиан , который не равен нулю, поскольку по условию теоремы решения образуют фундаментальную систему решений соответствующего ОЛДУ. При условии данная система линейных неоднородных алгебраических уравнений имеет единственное решение относительно неизвестных , которое обозначим как .

Таким образом, сумма линейной комбинации фундаментальных решений вида и частного решения Является решением, получена из общего решения при некоторых значениях Произвольных постоянных и по построению удовлетворяет начальным условиям, что и требовалось доказать.

Если известна фундаментальная система решений соответствующего ОЛДУ и, следовательно, его общее решение , то для определения частного решения НЛДУ порядка можно воспользоваться Методом Лагранжа вариации произвольных постоянных.

Этот метод заключается в том, что частное решение НЛДУ ищут в виде

Т. е. в виде линейной комбинации неизвестных функций и заранее вычисленных фундаментальных решений соответствующего ОЛДУ.

Предварительно находят производные из системы алгебраических уравнений следующего вида:

Определителем этой системы является Вронскиан , который не равен нулю при любом , поскольку решения образуют фундаментальную систему решений соответствующего ОЛДУ.

При условии данная система линейных неоднородных алгебраических уравнений имеет единственное решение относительно неизвестных , которое представим в виде равенств .

Интегрируя каждое из полученных равенств, получим набор первообразных для функций .

Окончательно, получаем функцию ,

Которая, как доказано в общей теории, является частным решением ЛНДУ при условии непрерывности на некотором интервале функций .

Отметим, что для произвольного НЛДУ порядка нет общего способа построения системы фундаментальных решений . Таким образом, методом Лагранжа можно воспользоваться только тогда, когда эту фундаментальную систему каким-либо способом удается найти. Если НЛДУ порядка имеет числовые коэффициенты , то фундаментальная система решений , соответствующего ОЛДУ, находится всегда и достаточно просто. В этом случае для нахождения частного решения всегда можно использовать метод Лагранжа.

Теорема (о наложении решений ЛНДУ).

Если правая часть ЛНДУ представлена в виде суммы нескольких функций, так что

, и есть частные решения неоднородных уравнений , то сумма этих частных решений есть некоторое частное решение исходного ЛНДУ.

Доказательство. Подставим функцию В исходное уравнение и убедимся в том, что эта функция действительно является решением ЛНДУ:

При выводе были использованы линейные свойства линейного дифференциального оператора и условия теоремы. Таким образом, теорема полностью доказана.

Частным случаем ЛНДУ являются линейные неоднородные дифференциальные уравнения порядка с постоянными числовыми коэффициентами вида .

Так как постоянные функции непрерывны на любом промежутке, то по теореме о структуре общего решения ЛНДУ для того, чтобы найти общее решение данного уравнения достаточно построить фундаментальную систему решений соответствующего однородного уравнения, найти некоторое частное решение ЛНДУ и представить общее решение в следующем виде:

Рассмотрим на примере ЛНДУ второго порядка с постоянными коэффициентами, как находится его общее решение с использованием метода Лагранжа для отыскания частного решения.

Пример. Найти общее решение уравнения .

На первом этапе ищется общее решение соответствующего однородного уравнения Его характеристическое уравнение имеет вид Корни характеристического уравнения находятся по общей формуле вычисления корней квадратного уравнения и в данном случае равны , .

В соответствии с общей теорией функции , являются линейно независимыми, и для уравнения второго порядка образует фундаментальную систему решений.

Таким образом, общее решение соответствующего однородного уравнения имеет вид

Заменим в общем решении Постоянные Неизвестными функциями И в соответствии с методом неопределенных коэффициентов будем искать частное решение НЛДУ в виде .

Предварительно для НЛДУ второго порядка решается система уравнений

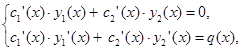
Линейная относительно производных неизвестных функций .

Для данного уравнения указанная система имеет вид

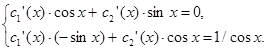
Определителем этой системы является Вронскиан который всегда отличен от нуля, что позволяет найти неизвестные по формулам Крамера

, .

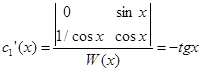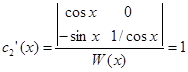Интегрируя полученные дифференциальные уравнения и выделяя первообразные их правых частей , , находим неизвестные функции в виде , . Отсюда, частное решение данного НЛДУ равно

Окончательно, общее решение данного уравнения записывается в виде

Пример. Найти общее решение уравнения .

На первом этапе ищется общее решение соответствующего однородного уравнения Его характеристическое уравнение имеет вид Корни характеристического уравнения находятся с использованием общей формулы вычисления корней квадратного уравнения и в данном случае равны , , .

В соответствии с общей теорией функции , , являются линейно независимыми, и для уравнения третьего порядка образует фундаментальную систему решений.

Таким образом, общее решение соответствующего однородного уравнения имеет вид

Заменим в общем решении Постоянные Неизвестными функциями И в соответствии с методом неопределенных коэффициентов Лагранжа будем искать частное решение НЛДУ в следующем виде:

Для данного НЛДУ третьего порядка система уравнений, линейная относительно производных неизвестных функций имеет вид:

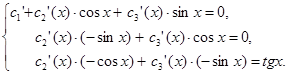
Определителем этой системы является Вронскиан

Который отличен от нуля, что позволяет найти неизвестные По формулам Крамера в следующем виде: , , .

Интегрируя полученные дифференциальные уравнения, находим неизвестные функции , , . Отсюда, частное решение данного НЛДУ равно .

Окончательно, общее решение данного уравнения записывается в виде

Пусть правая часть линейного неоднородного дифференциального уравнения порядка с постоянными числовыми коэффициентами имеет Специальный вид:

1) ,

2) ,

Где – вещественные числа, И– полиномы степеней и .

Как и ранее, чтобы найти общее решение данного уравнения достаточно построить фундаментальную систему решений соответствующего однородного уравнения, найти некоторое частное решение ЛНДУ и представить общее решение в виде .

Однако если правая часть ЛНДУ имеет специальный вид, то частное решение уравнения также имеет структуру, аналогичную правой части, и может быть найдено по Методу неопределенных коэффициентов. Этот метод несколько проще метода вариации произвольных постоянных, так как не включает в себя операцию интегрирования функций.

1) Рассмотрим вначале ЛНДУ с постоянными коэффициентами второго порядка со специальной частью первого вида .

В этом случае частное решение дифференциального уравнения ищем в виде

Т. е. выбираем полином той же степени, что и в правой части, только с неизвестными заранее коэффициентами , а число назначаем равным числу в правой части.

Показатель степенной функции выбирают равным нулю, если число не совпадает ни с одним корнем характеристического уравнения, и равным кратности корня характеристического уравнения в случае совпадения числа с каким-либо корнем.

Рассмотрим на конкретных примерах ЛНДУ второго порядка, как находится его общее решение с использованием метода неопределенных коэффициентов для отыскания частного решения .

Пример. Найти общее решение уравнения .

На первом этапе ищется общее решение соответствующего однородного уравнения . Его характеристическое уравнение имеет корни , . Следовательно, фундаментальная система решений имеет вид ,, а общее решение соответствующего однородного уравнения есть .

Для нахождения частного решения неоднородного уравнения воспользуемся методом неопределенных коэффициентов. Так как не совпадает ни с одним корнем характеристического уравнения, то и частное решение будем искать в виде

Вычислив производные , И подставив , и в исходное уравнение получим (после сокращения на ) следующее тождество:

Сравнивая коэффициенты обеих частей этого тождества, получим систему трех линейных уравнений для определения неизвестных коэффициентов:

Откуда .

Итак, , и, следовательно, общее решение уравнения имеет вид .

Пример. Найти общее решение уравнения .

На первом этапе ищется общее решение соответствующего однородного уравнения . Его характеристическое уравнение имеет двукратный корень . Следовательно, фундаментальная система решений имеет вид ,, а общее решение соответствующего однородного уравнения есть .

Для нахождения частного решения неоднородного уравнения воспользуемся методом неопределенных коэффициентов. Так как совпадает с двукратным корнем характеристического уравнения, то и частное решение будем искать в виде

Вычислив производные , И подставив , и в исходное уравнение получим (сократив на и сравнив коэффициенты при одинаковых степенях ) следующие значения для неопределенных коэффициентов: .

Следовательно, , а общее решение данного уравнения имеет вид .

2) Рассмотрим далее ЛНДУ с постоянными коэффициентами второго порядка со специальной частью второго вида .

В этом случае частное решение уравнения ищем в виде

Т. е. выбираем полиномы при косинусе и синусе наибольшей степени, из имеющихся в правой части, с неизвестными заранее коэффициентами и , а числа , назначаем равными числам , , стоящим в правой части.

Показатель степенной функции выбирают равным нулю, если комплексное число , не совпадает ни с одним комплексным корнем характеристического уравнения, и равным кратности комплексного корня характеристического уравнения в случае совпадения числа с каким-либо комплексным корнем.

Пример. Найти частное решение уравнения .

На первом этапе ищется общее решение соответствующего однородного уравнения . Его характеристическое уравнение имеет два различных комплексных корня ,. Следовательно, фундаментальная система вещественных решений имеет вид , , а общее решение соответствующего однородного уравнения есть .

Для нахождения частного решения неоднородного уравнения воспользуемся методом неопределенных коэффициентов. Так как комплексная пара сопряженных чисел правой части исходного уравнения совпадает с комплексной парой корней кратности один характеристического уравнения, то и частное решение будем искать в виде

Вычислив производные , И подставив , и в исходное уравнение получим следующее тождество: . Сравнивая коэффициенты при синусе и косинусе, найдем следующие значения для неопределенных коэффициентов: . Следовательно, , а общее решение данного уравнения имеет вид .

< Предыдущая		Следующая >