3.4. Линейные однородные дифференциальные уравнения

Линейные однородные дифференциальные уравнения (ЛОДУ) имеют самостоятельное значение, а также – вспомогательное значение в качестве первого этапа в процессе решения линейных неоднородных дифференциальных уравнений.

Теорема (о линейных свойствах решений ЛОДУ).

Если функции , заданные на некотором интервале , являются решениями линейного однородного дифференциального уравнения, то их линейная комбинация Также является решением.

Доказательство. Если линейное однородное дифференциальное уравнение записать с помощью линейного дифференциального оператора, то это уравнение будет иметь вид . Так как дифференциальный оператор обладает свойством линейности, то

, что и доказывает теорему.

Определение. Система решений ОЛДУ, заданных на некотором интервале , называется фундаментальной, если эти решения линейно независимы на интервале , а число этих решений равно порядку дифференциального уравнения.

Теорема (критерий фундаментальности решений).

Для того чтобы система решений ОЛДУ порядка с непрерывными на некотором интервале коэффициентами Была фундаментальной, необходимо и достаточно, чтобы Вронскиан системы был отличен от нуля во всех точках интервала .

Доказательство. Докажем достаточность условия теоремы. Если у системы решений ОЛДУ порядка , заданных на некотором интервале , Вронскиан не равен нулю во всех точках интервала , то по признаку независимости функций данная система является фундаментальной, что и доказывает достаточность условия теоремы.

Для доказательства необходимости условия теоремы, предположим обратное. Положим, что существует точка , где Вронскиан равен нулю, а система решений ОЛДУ порядка является линейно независимой.

Выберем числа , не все равные нулю, и такие, что они являются решениями однородной линейной системы уравнений

Это возможно по теореме о существовании нетривиального решения, так как определителем этой системы является Вронскиан , который по предположению равен нулю. Линейная комбинация решений Также является решением. Из вида построенной системы следует, что числа Есть коэффициенты решения задачи Коши с начальными условиями вида .

Но таким же начальным условиям удовлетворяет и нулевое решение . Так как по условию доказываемой теоремы коэффициенты ОЛДУ непрерывны на интервале , то справедлива теорема о существовании и единственности решения на интервале . Отсюда следует, что построенное решение и нулевое решение совпадают, т. е. , причем не все числа Одновременно равны нулю. Это означает, что решения линейно зависимы, хотя предполагалось обратное. Полученное противоречие завершает доказательство необходимости условия теоремы. Таким образом, теорема полностью доказана.

Теорема (о структуре общего решения ЛОДУ).

Если ОЛДУ порядка с непрерывными на некотором интервале коэффициентами имеет фундаментальную систему из решений, то линейная комбинация произвольных постоянных И Решений , является общим решением ОЛДУ.

Доказательство. В теореме о линейных свойствах ОЛДУ утверждается, что линейная комбинация Является решением. Докажем далее, что эта линейная комбинация является общим решением, т. е. в любой точке для допустимых начальных условий существует решение задачи Коши, которое получается из общего решения при некоторых значениях произвольных постоянных. Подставляя начальные условия в общее решение и его производные до - го порядка, получим систему линейных уравнений

Определителем этой системы является Вронскиан , который не равен нулю, поскольку по условию теоремы решения образуют фундаментальную систему. При условии данная система линейных неоднородных алгебраических уравнений имеет единственное решение относительно неизвестных , которое обозначим как . Линейная комбинация вида является решением, получена из общего решения при некоторых значениях Произвольных постоянных и по построению удовлетворяет начальным условиям. Таким образом, теорема полностью доказана.

Если начальные значения Удовлетворяют условиям теоремы Коши, то функция Является единственным решением задачи Коши.

Частным случаем линейных однородных дифференциальных уравнений являются ЛОДУ с постоянными коэффициентами вида ,

Где – некоторые числа.

Так как постоянные функции непрерывны на любом промежутке, то по теореме о структуре общего решения ОЛДУ для того, чтобы найти общее решение данного уравнения достаточно построить фундаментальную систему решений .

Как было предложено Л. Эйлером, будем искать частное решение ОЛДУ с постоянными коэффициентами в виде экспоненциальной функции , где – некоторое число. Дифференцируя эту функцию раз и подставляя полученные функции в решаемое дифференциальное уравнение получим следующие равенства:

.

Так как экспоненциальная функция строго положительна, то обязательно равен нулю полином -ой степени, т. е. . Полученное алгебраическое уравнением называют Характеристическим уравнением ОЛДУ.

Формально характеристическое уравнение ОЛДУ находят, подставляя в дифференциальное уравнение вместо Соответственно .

Таким образом, если некоторое число является решением данного характеристического уравнения ОЛДУ, то экспоненциальная функция является решением ОЛДУ.

Из основной теоремы алгебры следует, что характеристическое уравнение ОЛДУ имеет корней с учетом их кратности. Рассмотрим следующие варианты.

1. Все корней вещественные и различные.

Если ОЛДУ с постоянными коэффициентами имеет второй порядок, то характеристическое уравнение является квадратным уравнением вида . Каждому корню Соответствуют частные решения ,. Как было показано ранее в примере, эти функции являются линейно независимыми. Для уравнения второго порядка это означает, что система функций , образует фундаментальную систему решений ОЛДУ. Из теоремы о структуре общего решения ОЛДУ следует, что линейная комбинация Является общим решением ОЛДУ второго порядка с постоянными коэффициентами.

Пример. Решить ОЛДУ второго порядка .

Характеристическое уравнение данного ОЛДУ имеет вид . Оно имеет вещественные различные корни , . Каждому корню Соответствуют частные решения , , которые образуют фундаментальную систему решений.

Отсюда, есть общее решение ОЛДУ.

Доказано, что ОЛДУ с постоянными коэффициентами порядка в том случае, когда все корни характеристического уравнения вещественные и различные, имеет общее решение аналогичного вида .

Пример. Найти общее решение ОЛДУ третьего порядка .

Характеристическое уравнение данного ОЛДУ имеет вид .

Оно имеет вещественные различные корни , , .

Отсюда, есть общее решение данного ОЛДУ третьего порядка с постоянными коэффициентами.

2. Все корней вещественные, но среди них есть кратные.

Рассмотрим вначале и более подробно ОЛДУ с постоянными коэффициентами второго порядка. Его характеристическое уравнение является квадратным уравнением вида , которое может иметь один корень кратности два. Этому корню соответствует частное решение . Второе частное решение ищем в виде .

Подставим функцию в исходное дифференциальное уравнение. Тогда

.

В правой части последнего равенства первая скобка равна нулю, так как Есть корень характеристического уравнения, а вторая скобка равна нулю, так как в данном случае дискриминант квадратного уравнения равен нулю и, следовательно, .

Таким образом, показано, что предлагаемая функция есть решение.

Ранее в примере было показано, что функции , являются линейно независимыми. Для уравнения второго порядка это означает, что система функций , образует фундаментальную систему решений ОЛДУ.

Из теоремы о структуре общего решения ОЛДУ следует, что линейная комбинация

Является общим решением ОЛДУ второго порядка с постоянными коэффициентами.

Пример. Решить ОЛДУ второго порядка .

Характеристическое уравнение данного ОЛДУ имеет вид . Оно имеет один вещественный корень кратности два. Для уравнения второго порядка это означает, что система функций , образует фундаментальную систему решений ОЛДУ. Из теоремы о структуре общего решения ОЛДУ следует, что линейная комбинация Является общим решением ОЛДУ второго порядка с постоянными коэффициентами.

В общем случае дифференциального уравнения порядка каждому простому корню соответствует одно частное решение вида , а каждому корню кратности соответствует частных решений вида .

Доказано, что общее решение ОЛДУ с постоянными коэффициентами порядка в данном случае представляет собой линейную комбинацию произвольных постоянных И частных фундаментальных решений указанных выше видов.

Пример. Найти общее решение ОЛДУ с постоянными коэффициентами четвертого порядка .

Характеристическое уравнение имеет один простой корень и корень кратности три.

Общее решение данного уравнения в соответствии с изложенной теорией имеет вид

.

3. Среди корней могут быть как вещественные, так и комплексные корни.

Если характеристическое уравнение имеет вещественные коэффициенты, то, как было доказано ранее в теории алгебраических уравнений, каждому комплексному корню обязательно соответствует сопряженный корень .

Рассмотрим вначале ОЛДУ с постоянными вещественными коэффициентами второго порядка. Если его характеристическое уравнение содержит комплексный корень вида , то второй корень обязательно имеет вид . Частными решениями такого ОЛДУ являются функции , .

Так как исходное ОЛДУ имеет вещественные коэффициенты, то полезно наряду с решениями, представленными в комплексной форме, иметь вещественные решения.

Воспользуемся формулами Эйлера, и представим решения в тригонометрическом виде

.

Далее, построим линейные комбинации этих решений следующего вида:

, .

По теореме о линейных свойствах решений данные функции также являются решениями исходного ОЛДУ. Составим Вронскиан для этих решений

.

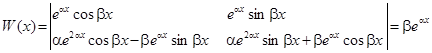Так как экспоненциальная функция строго положительна, а характеристическое уравнение имеет комплексные корни (, то Вронскиан всегда отличен от нуля. В соответствии с критерием фундаментальности, решения , являются линейно независимыми, и для уравнения второго порядка образует фундаментальную систему решений.

Из теоремы о структуре общего решения ОЛДУ следует, что линейная комбинация

Является общим решением ОЛДУ второго порядка с постоянными коэффициентами, если его характеристическое уравнение имеет два комплексных корня.

Пример. Решить ОЛДУ второго порядка .

Характеристическое уравнение данного ОЛДУ имеет вид . Уравнение имеет пару комплексно-сопряженных корней и . Из общей теории следует, что решения , являются линейно независимыми и для уравнения второго порядка образует фундаментальную систему решений. Из теоремы о структуре общего решения ОЛДУ следует, что линейная комбинация является общим решением данного ОЛДУ второго порядка с вещественными коэффициентами.

В общем случае каждой паре простых комплексно-сопряженных корней соответствует два частных решения вида , , а каждой паре корней кратности соответствует частных решений следующего вида:

,

.

Доказано, что общее решение ОЛДУ порядка с постоянными вещественными коэффициентами в общем случае представляет собой линейную комбинацию произвольных постоянных И фундаментальных решений всех указанных выше видов.

Пример. Решить ОЛДУ пятого порядка .

Характеристическое уравнение данного ОЛДУ имеет вид . Оно имеет один вещественный корень и пару комплексно-сопряженных корней , Кратности два.

В соответствии с общей теорией система функций , , Является фундаментальной системой решений, а линейная комбинация есть общее решение данного ОЛДУ пятого порядка с вещественными коэффициентами.

< Предыдущая		Следующая >