3.3. Линейные дифференциальные уравнения высших порядков

Дифференциальное уравнение -го порядка называют Линейным, если его можно представить в виде , содержащем неизвестную функцию и ее производные до порядка включительно линейным образом.

Если правая часть уравнения Тождественно равна нулю, то линейное уравнение называют Однородным, если же – Неоднородным.

Левую часть уравнения обозначают символом и называют Линейным дифференциальным оператором. Действительно, этот оператор преобразует множество -раз дифференцируемых функций в себя и является линейным, что следует из соответствующих свойств производных. Таким образом, справедливо следующее свойство:

,

Которое читают: «Линейный оператор от линейной комбинации функций равен линейной комбинации операторов». Задача Коши для дифференциальных уравнений высших порядков была сформулирована ранее, а терема Коши в данном случае имеет следующий вид.

Теорема Коши (о существовании и единственности решения задачи Коши).

Если в линейном, неоднородном дифференциальном уравнении -Го порядка Функции непрерывны на некотором интервале , то для любой точки на интервале существует и притом единственное решение этого уравнения, удовлетворяющее начальным условиям.

Рассмотрим далее как строится общее решение линейного уравнения -го порядка. Отметим, что множество -раз дифференцируемых функций образует линейное пространство. Это позволяет пользоваться общими определениями линейно зависимых и линейно независимых векторов применительно к таким функциям. В частности, для проверки линейной зависимости некоторой системы функций полезна следующая теорема.

Теорема (необходимое условие зависимости функций).

Если функции , заданные на некотором интервале , линейно зависимы и имеют на интервале производные до порядка включительно, то определитель Вронского (Вронскиан) равен нулю при любых , т. е.

.

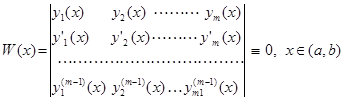Доказательство. Так как по условию теоремы функции линейно зависимы на интервале , то существуют числа не все равные нулю такие, что , т. е. что линейная комбинация функций равна нулевой функции. Дифференцируя это равенство Раз, получим систему уравнений

Неизвестными этой системы являются числа , а матрица коэффициентов при любом по форме соответствует определителю Вронского. Данная система является однородной и по условию теоремы имеет ненулевое решение. Как следует из теории линейных алгебраических уравнений, это возможно только в том случае, когда определитель системы, в данном случае Вронскиан, равен нулю при всех , что и требовалось доказать. По закону контрпозиции из данной теоремы выводится следствие.

Следствие (признак независимости системы функций).

Если хотя бы в одной точке интервала Определитель Вронского отличен от нуля, то система функций линейно независима на интервале .

Пример. Покажем, что функции линейно независимы на любом числовом множестве. Вронскиан данной системы функций имеет значение

.

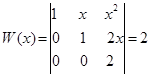Так как Вронскиан отличен от нуля при любых , то по признаку независимости системы функций отсюда следует, что функции линейно независимы на любом числовом множестве.

Пример. Рассмотрим функции , заданные на всей вещественной оси. Вронскиан данной системы функций имеет вид

.

Если выполняется условие , то Вронскиан отличен от нуля при любых . По признаку независимости системы функций отсюда вытекает, что функции Линейно независимы на любом подмножестве всех вещественных чисел. Если же , то Вронскиан равен нулю при любых . Это означает, что не существует такого множества, где функции Были бы линейно независимы.

Пример. Рассмотрим функции , заданные на всей вещественной оси. Покажем, что эти функции являются линейно независимыми на своей естественной области определения. Составим линейную комбинацию этих функций . Экспоненциальная функция строго положительна, а полином второй степени тождественно равен нулю, если все числа Одновременно равны нулю. Отсюда тождественное равенство нулю данной линейной комбинации возможно только при условии , что и означает по определению линейную независимость данной системы функций на всей вещественной оси.

< Предыдущая		Следующая >