3.2. Дифференциальные уравнения, допускающие понижение порядка

Дифференциальные уравнения высших порядков в общем случае не имеют стандартных методов отыскания точного решения. Рассмотрим некоторые виды дифференциальных уравнений высших порядков, которые допускают понижение порядка и сводятся в итоге к дифференциальным уравнениям первого порядка.

1) Уравнение вида С правой частью, зависящей только от аргумента .

Порядок уравнения можно понизить на единицу, положив . Тогда, по определению производных высших порядков, получим . Решая дифференциальное уравнение первого порядка , получим его общее решение в виде

, где – одна из первообразных функции . Подставляя полученное общее решение в уравнение , перейдем к дифференциальному уравнению , порядок которого на единицу меньше, чем порядок исходного уравнения. Продолжая этот процесс, можно получить общее решение исходного уравнения в виде , которое обязательно содержит аргумент И произвольных постоянных .

Пример. Найти общее решение ДУ второго порядка и его частное решение, удовлетворяющее начальным условиям , .

Интегрируя правую часть исходного ДУ первый раз, получаем дифференциальное уравнение первого порядка . Повторное интегрирование полученного дифференциального уравнения первого порядка дает общее решение исходного уравнения в виде .

Подставив в полученное общее решение и выражение для первой производной начальное значение аргумента , получим два линейных уравнения относительно произвольных постоянных :

Отсюда, окончательно, решение задачи Коши имеет вид .

2) Уравнение вида , Которое не содержит явно искомую функцию и ее производные до порядка включительно.

Порядок уравнения можно понизить на Единиц, положив . Тогда, по определению производных высших порядков, получим

.

Подставляя полученные равенства в исходное уравнение, переходим к уравнению Относительно неизвестной функции . Предположим, что для полученного уравнения можно найти общее решение . Подставляя это решение в уравнение , приходим к уравнению , которое решается относительно функции по предложенной в пункте один схеме.

Пример. Найти частное решение ДУ третьего порядка , удовлетворяющее начальным условиям , ,.

Данное уравнение не содержит в явном виде искомой функции и ее первой производной . В соответствии с предложенным методом, положим и найдем . Подставляя полученные равенства в исходное уравнение, переходим к уравнению относительно неизвестной функции . Это линейное уравнение первого порядка, которое решается по методу Лагранжа или методу Бернулли. Не рассматривая в данном примере ход решения этого уравнения, сразу представим его общее решение . Используя начальное условие , находим . Следовательно , и получено уравнение относительно функции , правая часть которого зависит только от аргумента . Интегрируя это уравнение первый раз, находим . Начальное условие позволяет определить . Интегрируя еще раз уравнение , получаем , а из условия находим, что произвольная постоянная . Итак, искомое частное решение есть .

3) Уравнение вида , Которое не содержит явно независимой переменной .

Порядок уравнения можно понизить на единицу, положив . Тогда, по правилу дифференцирования сложной функции, получим

,, и т. д.

Подставляя полученные равенства в исходное уравнение, переходим к уравнению относительно неизвестной функции , которое имеет порядок . Предположим, что для полученного уравнения можно найти общее решение .

Подставляя это решение в уравнение , приходим к уравнению , которое является уравнением с разделяющимися переменными и решается относительно функции по разработанным для таких уравнений методам.

Пример. Найти частное решение ДУ второго порядка 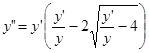, удовлетворяющее начальным условиям , .

Данное уравнение не содержит явно независимой переменной . В соответствии с предложенным методом, положим и найдем . Подставляя полученные равенства в исходное уравнение, переходим к уравнению относительно неизвестной функции . Это однородное уравнение первого порядка, которое решается с помощью подстановки . Переходя к переменным , получим дифференциальное уравнение . Разделяя переменные, приведем это уравнение к виду . Его общее решение имеет вид или. . Используя начальные условия ,, находим . Тогда или . Возвращаясь к старым переменным, получим или . Это уравнение с разделенными переменными, которое имеет общий интеграл . Из условия находим, что произвольная постоянная . Итак, искомое частное решение есть .

< Предыдущая		Следующая >