2.5. Уравнения в полных дифференциалах

Дифференциальное уравнение первого порядка вида называют Уравнением в полных дифференциалах, если в области Существования решений этого уравнения выполняется равенство .

Как следует из теории криволонейных интегралов, при выполнении данных условий общий интеграл уравнения в полных дифференциалах определяется по одной из формул:

,

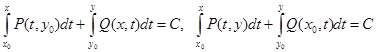Где точки и соединяющие их ломаные принадлежат области .

Пример. Найти общий интеграл дифференциального уравнения первого порядка , представленного в дифференциальной форме.

Обозначим . Найдем первые частные производные , и убедимся, что условия существования уравнения в полных дифференциалах выполняются в области . Выберем начальную точку , равной нулевой точке . Воспользуемся для вычисления общего интеграла данного дифференциального уравнения первой из рекомендуемых формул

.

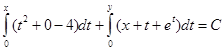Вычисляя интегралы с переменным верхним пределом, получим общий интеграл данного уравнения в полных дифференциалах в следующем виде:

.

< Предыдущая		Следующая >