2.4. Линейные дифференциальные уравнения

Дифференциальное уравнение первого порядка называют Линейным, если его можно представить в виде , содержащем неизвестную функцию и ее производную Линейным образом.

Если правая часть уравнения Тождественно равна нулю, то линейное уравнение называют Однородным, если же – Неоднородным.

Рассмотрим два метода решения линейного неоднородного уравнения.

1) Метод Лагранжа вариации произвольной постоянной.

В соответствии с методом Лагранжа сначала линейное неоднородное уравнение Заменяют соответствующим однородным уравнением .

Однородное уравнение всегда приводится к уравнению с разделенными переменными , путем деления на функцию При условии . Общий интеграл этого уравнения имеет вид , где функция является некоторой первообразной функции . Преобразуем общий интеграл приведенного уравнения сначала к виду 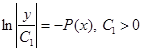, а затем, потенцируя, к виду . Освобождаясь от знака модуля, найдем общее решение в виде .

В процессе разделения переменных выполнялось деление обеих частей приведенного уравнения на функцию , в результате чего могло быть потеряно решение . После подстановки функции в приведенное уравнение, мы убеждаемся, что действительно является решением. Это решение тем или иным способом должно быть включено в множество всех решений дифференциального уравнения. В нашем случае решение можно включить в общее решение , введя вместо параметра произвольную постоянную , принимающую любые вещественные значения. Таким образом, окончательно получим решение приведенного уравнения в виде .

Произвольную постоянную в полученном решении заменяют на некоторую дифференцируемую функцию , и ищут решение исходного уравнения в форме . Производная этого решения имеет вид .

Подставляя функции и В исходное уравнение, получим уравнение относительно неизвестной функции в виде .

Если общее решение приведенного уравнения и производные функций найдены правильно, то слагаемые, содержащие функцию , обязательно равны между собой, и мы приходим к равносильному уравнению . Это уравнение имеет общее решение вида , где функция есть первообразная функции . Подставляя полученное выражение для в решение , находим решение исходного линейного неоднородного уравнения в виде .

Пример. Решить уравнение .

Так как функции и Входят в наше уравнение линейным образом, а в правой части уравнения имеется функция , то это – линейное неоднородное уравнение первого порядка. Применим метод вариации произвольной постоянной.

Рассмотрим сначала соответствующее однородное линейное уравнение . Общее решение приведенного уравнения имеет вид .

Следовательно, общее решение исходного уравнения ищем в виде .

Подставляя И в решаемое уравнение, получим или . Отсюда . Окончательно, общее решение исходного уравнения имеет вид .

2) Метод подстановки Бернулли.

Будем искать решение нашего линейного уравнения в виде произведения двух функций, т. е. выполним подстановку . Это возможно, так как любую функцию можно тождественно представить в виде .

Вычислим производную И подставляя функции и В исходное уравнение, получим уравнение . Найдем функцию В таком виде, чтобы выражение в скобках было равно нулю, т. е. решим дифференциальное уравнение Относительно функции . Рассматривая метод Лагранжа, мы уже решали аналогичное уравнение Относительно функции. Отсюда, общее решение нашего уравнения имеет вид , где функция является некоторой первообразной функции . Выбирая произвольную постоянную равной единице, мы получим искомую функцию в виде .

Подставляя найденную функцию в уравнение , получим новое уравнение относительно неизвестной функции в виде . Уравнение этого типа также решалось ранее, так что его общее решение можно выписать в виде , где функция – первообразная функции .

Подставляя полученные выражения для И в подстановку , находим, окончательно, решение исходного линейного, неоднородного уравнения в виде .

Пример. Решить уравнение .

Так как функции и Входят в наше уравнение линейным образом, а в правой части уравнения имеется функция , то это – линейное, неоднородное уравнение первого порядка. Применим метод подстановки Бернулли.

Подставляя функции и В исходное уравнение, получим уравнение . Найдем функцию В таком виде, чтобы выражение в скобках было равно нулю, т. е. решим дифференциальное уравнение Относительно функции . Разделяя переменные и интегрируя, найдем решение в виде .

Подставляя найденную функцию в уравнение , и учитывая, что при второе слагаемое в левой части уравнения тождественно равно нулю, получим новое уравнение относительно неизвестной функции в виде . Уравнение этого типа также решалось ранее, так что его общее решение можно выписать в виде .

Окончательно, общее решение исходного линейного уравнения имеет вид

.

Отметим, что и метод Лагранжа, и метод Бернулли имеют самостоятельное значение. В дальнейшем метод Лагранжа используется для решения дифференциальных уравнений высших порядков. Метод Бернулли, в частности, позволяет решать нелинейное уравнение специального вида , называемое уравнением Бернулли.

< Предыдущая		Следующая >