2. 2. Дифференциальные уравнения с разделяющимися переменными

Рассмотрим дифференциальное уравнение первого порядка , разрешенное относительно первой производной. Предположим, что функция непрерывна на некотором интервале . Задача нахождения решений дифференциального уравнения в данном случае решается с помощью понятия неопределенного интеграла . Поскольку все первообразные отличаются одна от другой на постоянную , то любое решение уравнения можно записать в виде 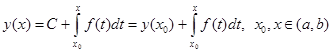. Здесь в качестве первообразной выбран интеграл с переменным верхним пределом 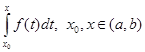, который всегда существует для непрерывных функций.

Построенное множество функций является общим решением данного дифференциального уравнения. Действительно, если взять производную от любой функции , то

,

Т. е. функция при любом значении произвольной постоянной является решением.

Задачу Коши для данного уравнения можно формулировать для тех точек Открытого множества , которые лежат внутри естественной области определения правой части дифференциального уравнения , т. е. .

Множество есть область на плоскости , а функция двух переменных непрерывна на этой области . Частная производная по переменной на этой области равна нулю, так как .

Таким образом, множество можно выбрать как область , в которой данное уравнение имеет единственное решение задачи Коши.

Отсюда, для начальных значений решение задачи Коши 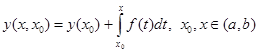единственно и получается из построенного общего решения 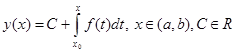при значении .

Таким образом, общее решение данного уравнения имеет вид неопределенного интеграла , где – любая первообразная функции , – произвольная постоянная, или вид 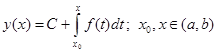, где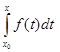 – интеграл с переменным верхним пределом.

Решение задачи Коши данного дифференциального уравнения имеет вид 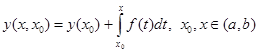. Оно существует и единственно на интервале .

Пусть дифференциальное уравнение первого порядка представлено в Дифференциальной форме и имеет вид . В этом уравнении левая часть зависит только от переменной , а правая – только от переменной . Такие дифференциальные уравнения называют Уравнениями с разделенными переменными.

Предположим далее, что функции , непрерывны на некоторых интервалах , И имеют там первообразные, . Тогда можно проинтегрировать левую часть уравнения по переменной , а правую часть – по переменной и получить общий интеграл дифференциального уравнения в виде . Произвольную постоянную можно включать как в левую часть общего интеграла, так и в правую часть, стараясь представить общее решение в достаточно компактном виде.

В предположении, что функция Не равна нулю на интервале , представим данное уравнение в виде, разрешенном относительно производной , а именно . Множество существования и единственности решения задачи Коши будем строить по определению, т. е. как открытое связное множество, где правая часть и производная правой части 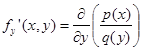непрерывны.

Пример. Решить уравнение с разделенными переменными .

Интегрируем левую и правую части данного уравнения и получаем общий интеграл уравнения в виде .

Представим данное уравнение в виде, разрешенном относительно производной . Правая часть непрерывна на всей плоскости , производная правой части также непрерывна на всей плоскости . Из теоремы Коши следует, что начальную точку Можно выбирать любой. Возьмем, в частности . Тогда, подставляя выбранные начальные значения в общий интеграл, получим . Отсюда решение данной задачи Коши будет иметь вид .

Уравнения с разделенными переменными в чистом виде встречаются довольно редко. Однако существуют так называемые уравнения с разделяющимися переменными, которые можно привести к уравнениям с разделенными переменными.

Пусть в дифференциальном уравнении Правая часть представлена в виде произведения функций, каждая из которых зависит только от одной переменной, т. е. дифференциальное уравнение имеет вид .

В предположении, что , это уравнение можно представить в виде уравнения с разделенными переменными И решить его по предложенной ранее схеме.

Может оказаться, что обычное уравнение имеет хотя бы один действительный корень . В этом случае постоянная функция является решением исходного дифференциального уравнения, что проверяется непосредственной подстановкой. Это решение могло быть потеряно при делении на функцию И должно быть включено в множество всех решений дифференциального уравнения.

Пример. Решить уравнение с разделяющимися переменными .

Разделяя переменные, мы придем к уравнению . После интегрирования левой и правой части уравнения с разделенными переменными получаем общий интеграл уравнения в виде . Для удобства потенцирования преобразуем решение к виду , а произвольную постоянную представим в логарифмической форме, положив . Тогда и, потенцируя, получаем общий интеграл в виде . Так как параметр может принимать как положительные, так и отрицательные значения, то множество решений вида совпадает с множеством решений более простого вида .

Поделив левую и правую части общего интеграла на функцию косинуса, получим окончательно общее решение исходного дифференциального уравнения в виде .

В процессе разделения переменных выполнялось деление обеих частей исходного дифференциального уравнения на функцию , в результате чего могло быть потеряно решение . После подстановки функции в исходное уравнение, мы убеждаемся, что действительно является решением. Это решение тем или иным способом должно быть включено в множество всех решений дифференциального уравнения. В нашем случае решение Можно включить в общее решение , введя вместо параметра параметр , принимающий любые вещественные значения. Таким образом, окончательно получим общее решение данного уравнения в виде .

Пример. Решить уравнение с разделяющимися переменными .

Разделяя переменные при, мы придем к уравнению . После интегрирования получаем общий интеграл уравнения в виде и, соответственно, равносильное ему общее решение в виде. При делении обеих частей исходного дифференциального уравнения на функцию было потеряно решение . Это решение не может быть получено из общего решения ни при каком значении произвольной постоянной, поэтому оно должно быть отдельно добавлено к общему решению и войти в полное множество решений дифференциального уравнения.

Покажем, что решение является особым. В соответствии с теоремой Коши в область Входят те точки плоскости , где существует и непрерывна правая часть Дифференциального уравнения, и те точки плоскости, где существует и непрерывна частная производная , т. е. множество .

Учитывая требование связности множества , обычно выбирают область состоящей только из тех точек плоскости, которые лежат строго выше или строго ниже оси . Таким образом, все точки плоскости, задаваемые уравнением , являются особыми, а решение есть особое решение.

В тех случаях, когда требуется решить задачу Коши вида ,

, при условии, что функции , являются непрерывными, удобно частный и общий интегралы дифференциального уравнения при Представлять в виде:

, ,

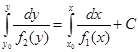Где в каждой формуле слева и справа от знака равенства в качестве первообразных выбраны интегралы с переменным верхним пределом.

Пример. Решить задачу Коши вида .

Разделяя переменные при , мы придем к уравнению . После интегрирования 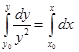получим частный интеграл уравнения в виде . После преобразования частного интеграла можно получить частное решение в виде .

При стремлении переменной к значению знаменатель частного решения стремится к нулю, а само решение стремится к бесконечности. Этот пример показывает, что при выполнении условий теоремы Коши гарантируется существование ограниченного решения только в малой окрестности начальной точки.

Область существования и единственности решения задачи Коши в нашем примере совпадает с множеством всех точек плоскости. Непосредственная проверка показывает, что функция Является решением. Так как у рассматриваемого уравнения нет особых точек, то оно не может иметь и особых решений, поэтому решение не особое.

Пусть дифференциальное уравнение первого порядка представлено в Дифференциальной форме и имеет вид . В этом уравнении в левой и правой частях стоят функции, представленные как произведение функций, каждая из которых зависит только от одной переменной или.

В предположении, что , это уравнение можно поделить на произведение и представить в виде дифференциального уравнения с разделенными переменными , которое решается по предложенной ранее схеме.

Пример. Решить дифференциальное уравнение с разделяющимися переменными, представленное в дифференциальной форме .

В предположении, что , это уравнение можно поделить на произведение и представить в виде дифференциального уравнения с разделенными переменными . Проинтегрировав это дифференциальное уравнение с разделенными переменными, находим его общий интеграл в виде

В процессе разделения переменных выполнялось деление обеих частей исходного дифференциального уравнения на функцию , в результате чего могли быть потеряны решения , . После подстановки функций , в исходное уравнение, мы убеждаемся, что , действительно являются решениями. Эти решения должны быть включены в множество всех решений дифференциального уравнения.

Проверим, являются ли эти решения особыми. Для этого запишем наше дифференциальное уравнение в канонической форме . Множество точек плоскости, таких что входит в множество особых точек нашего уравнения. Найдем далее те точки плоскости, где существует и непрерывна частная производная , т. е. множество точек плоскости вида .

Окончательно, область равна множеству , а, соответственно, множество особых точек равно .

Решение целиком состоит из особых точек, и по определению является особым. Решение не состоит из особых точек и, соответственно, не является особым. Подчеркнем, что оба решения должны быть включены в множество всех решений дифференциального уравнения.

Пусть дифференциальное уравнение имеет следующий вид:

,

Где параметры есть некоторые числа. Это уравнение путем замены Сводится к дифференциальному уравнению с разделяющимися переменными.

Действительно, . Отсюда можно получить уравнение с разделенными переменными Относительно переменных . Решая это уравнение и выполняя обратную подстановку, получаем общий интеграл исходного уравнения.

< Предыдущая		Следующая >