36. Пример решения биматричной игры

Формулировка игры “Борьба за рынки”

Небольшая фирма (игрок 1) намерена сбыть крупную партию товара на одном из двух рынков, контролируемых другой, более крупной фирмой (игрок 2). Для этого оно может предпринять на одном из рынков соответствующие действия (например, развернуть рекламную кампанию). Господствующий на рынках игрок 2 может попытаться воспрепятствовать этому, предприняв на одном из двух рынков предупредительные меры. Игрок 1, не встретивший на рынке препятствий, захватывает его; встретившись с сопротивлением – терпит поражение. Выборы фирмами рынков являются их чистыми стратегиями.

Пусть проникновение игрока 1 на первый рынок более выгодно для него, чем проникновение на второй, но борьба за первый рынок требует больших средств. Например, победа игрока 1 на первом рынке принесет ему вдвое больший выигрыш, чем на втором, но зато поражение на первом рынке полностью его разоряет (проигрыш равен 10), а игрока 2 избавляет от конкурента (выигрыш равен 5).

Описанная биматричная игра может быть задана матрицами выигрышей

Решение игры. В соответствии с выражениями (5.6) и (5.7) приемлемыми ситуациями для игрока 1 будут те, которые удовлетворяют условиям

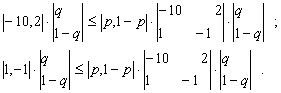
Рассмотрим три случая:

А) р=1 (X=|1, 0|). В соответствии с выражением (5.10) имеем

Откуда .

Б) р = 0 (X=|0, 1|). В соответствии с выражением (5.11) имеем

Или .

В) 0< Р<1 (X=|Р, 1 – Р|). В соответствии с выражением (5.12) или в развернутом виде (5.19) получаем

Приемлемые ситуации для игрока 2 в соответствии с выражениями (5.26), (5.27) и (5.27) следующие:

А)

Б)

В)

Множества всех приемлемых ситуаций игрока 1 и игрока 2 изображены на рис. 5.5 (для игрока 2 соответствующее множество показано пунктиром).

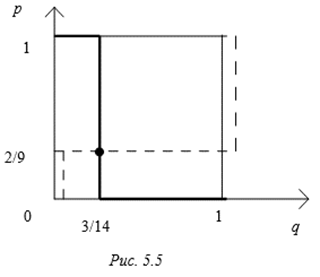
Зигзаги приемлемых ситуаций пересекаются в единственной точке , которая и оказывается единственной ситуацией равновесия. Эта ситуация равновесия является ситуацией равновесия в смешанных стратегиях. Таким образом, оптимальными стратегиями по Нэшу являются и . При этом цена игры для игрока 1

.

Цена игры для игрока 2

.

< Предыдущая		Следующая >