35. Решение биматричных игр

Рассмотрим вначале биматричную игру 2х2 с матрицами выигрышей

,

Соответственно игроков 1 и 2. Как и в случае матричных игр, смешанные стратегии полностью описываются вероятностями p и q выбора игроками своих первых чистых стратегий (вторые чистые стратегии выбираются, очевидно, с вероятностями 1-p и 1-q.

Опишем порознь множество приемлемых ситуаций, для каждого из игроков и изобразим эти множества на единичном квадрате P, q, где pÎ[0,1] и qÎ[0,1].

Начнем с описания ситуаций, приемлемых в игре для игрока 1.

Приемлемость ситуации (X, Y) для игрока 1 в биматричной игре означает, что

; (5.6)

, (5.7)

Где А1 и А2 – вектор строки, соответствующие первой и второй строке матрицы А, соответственно.

Подчеркнем, что эти условия приемлемости никак не связаны с матрицей В выигрышей игрока 2. Поэтому они будут совпадать с аналогичными условиями матричной игры с платежной матрицей А.

Приемлемость ситуации (X, Y) для игрока 2 означает, что

(5.8)

(5.9)

Где В1 и В2 – вектор-столбцы, соответствующие первому и второму столбцу матрицы В, соответственно.

В общем случае, Х=Ip, 1 – pI. Рассмотрим три случая:

А) р = 1, (Х=|1,0|). Тогда выражение (5.6) превращается в тождественное равенство, а условием приемлемости данной ситуации для игрока 1 оказывается неравенство (5.7). Для рассматриваемого случая его можно записать как

; (5.10)

Б) р = 0 (Х=|1,0|). В этом случае выражение (5.7) превращается в тождественное равенство, а условием приемлемости данной ситуации для игрока 2 оказывается неравенство (5.6). Для рассматриваемого случая оно имеет вид

; (5.11)

В) 0< р <1 (Х=Ip, 1 - pI). В этом случае оба неравенства (5.6) и (5.7) превращаются в равенство, и условием приемлемости становится

. (5.12)

Опишем ситуации приемлемости (5.10), (5.11) и (5.12) в развернутом виде. Так как

То соотношения (5.10), (5.11) и (5.12) можно соответственно записать как

(5.14)

(5.15)

(5.16)

Таким образом, приемлемые для игрока 1 ситуации (X, Y) могут быть одного из трех типов:

(5.17)

(5.18)

(5.19)

Неравенства (5.17) и (5.18) верны в случае, если а11 + а22 – а12 – а21 > 0. Если а11 + а22 – а12 – а21 < 0, то знак неравенства в соотношениях (5.17) и (5.18) необходимо поменять на противоположный.

Если величина а11 + а22 – а12 – а21 = 0, а а22 – а12 ¹ 0, то (5.19) не имеет место, поэтому будет выполняться или (5.17) и (5.18), и притом со знаком строгого неравенства.

Если же а11 + а22 – а12 – а21 = 0 и а22 – а12 = 0, то все условия (5.17), (5.18) и (5.19) выполняются тождественно, и приемлемыми для игрока 1 будут вообще все ситуации.

Описание ситуаций приемлемости в развернутом виде для игрока 2 получаем аналогично из неравенств (5.8) и (5.9).

В общем случае Y=|q, 1-q|. Для трех случая получаем:

А) q=1 (Y=|1,0|). В этом случае приемлемость ситуации (X, Y) равносильна неравенству

(5.20)

Или в развернутом виде

|p, 1-p|

. (5.21)

Б) q=0 (Y=|0,1|). В этом случае приемлемость ситуации (X, Y) определяется неравенством

(5.22)

Или в развернутом виде

. (5.23)

В) 0<q<1 (Y = |q,1–q|). Условие приемлемости

(5.24)

В развернутом виде

. (5.25)

Таким образом, приемлемые для игрока 2 ситуации (X, Y) могут быть одного из трех типов:

(5.26)

(5.27)

(5.28)

Вновь подчеркнем, что неравенства (5.26) и (5.27) справедливы, если их знаменатель больше нуля. Если в11 + в22 – в12 – в21 < 0, то знак неравенства в выражениях (5.26) и (5.27) необходимо поменять на противоположный.

Для определения ситуаций, приемлемых одновременно как для первого, так и для второго игроков, удобно все найденные приемлемые ситуации представить на единичном квадрате (рис. 5.3).

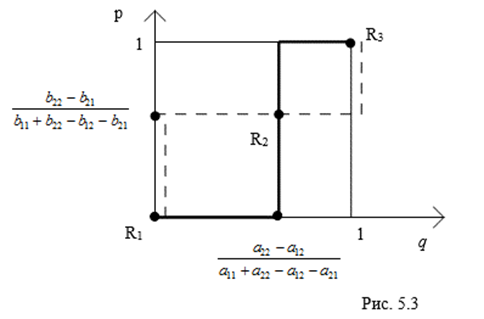
Для случаев, когда А11 + А22 – А12 – А21 ¹ 0 и B11 + B22 – B12 – B21 ¹ 0 приемлемые ситуации игроков 1 и 2 составляют трехзвенные зигзаги. Причем, ситуации равновесия во вполне смешанных стратегиях игрока 2 совпадают с поведением игрока 2 в матричной игре с матрицей выигрыша А, а поведение игрока 1 – с поведением игрока 1 в матричной игре с матрицей выигрышей В.

Таким образом, описанное равновесное поведение игроков оказывается ориентированным не столько на максимализацию собственного выигрыша, сколько на минимизацию выигрыша противника. Так, “антагонизм поведения” может возникнуть и при отсутствии “антагонизма интересов”.

В приведенном на рис. 5.3 решении игры три ситуации равновесия, соответствуют точкам R1, R2, R3.

Если бы зигзаги приемлемых ситуаций были одинаковой ориентации, как показано на рис. 5.4, то пересечение приемлемых ситуаций игрока 1 и игрока 2 состояло бы из одной точки R.

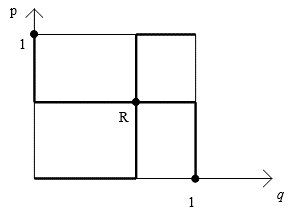
Рис. 5.4

При решении биматричных игр большей размерности необходимо решать большую систему линейных неравенств, определяемых выражениями (5.6), (5.7) и (5.8), (5.9), а затем таким же конечно-рациональным путем находить точки пересечения приемлемых ситуаций игрока 1 и игрока 2. Причем, любая конечная бескоалиционная игра имеет конечное и нечетное чисто ситуаций равновесия (решений игры). Поиск ситуаций равновесия в этом случае следует осуществлять с применением ПЭВМ.

< Предыдущая		Следующая >