34. Описание биматричных игр
Пусть в биматричной игре игрок 1 имеет m чистых АІ, ![]() , а игрок 2 имеет n чистых стратегий ВJ,
, а игрок 2 имеет n чистых стратегий ВJ, ![]() и в каждой ситуации (Ai, Bj) игрок 1 получает выигрыш aij, а игрок 2 – выигрыш bij. Значение обеих функций выигрыша игроков естественно представить в виде пары матриц
и в каждой ситуации (Ai, Bj) игрок 1 получает выигрыш aij, а игрок 2 – выигрыш bij. Значение обеих функций выигрыша игроков естественно представить в виде пары матриц
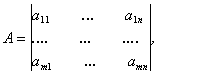

Поэтому такие игры и называются биматричными. Используют также запись платежных матриц А и В в следующем виде:
|
А11 b11 |
......... |
A1n b1n | ||
|
........ |
......... |
........ | ||
|
Am1 bm1 |
......... |
Amn bmn |
Где “северо-западное” число в каждой клетке обозначает выигрыш первого игрока, а “юго-восточное” – выигрыш второго игрока.
Смешанные стратегии X и Y, естественно, понимаются как векторы, причем
![]() и
и ![]() .
.
Выигрыш игроков 1 и 2 при применении смешанных стратегий равны:
![]()
![]()
Где Т – означает транспонирование, т. е. вектор строка записывается как вектор столбец; ![]() - смешанные стратегии игроков 1 и 2 соответственно.
- смешанные стратегии игроков 1 и 2 соответственно.
Определение ситуации равновесия для случая биматричной игры приобретает следующую формулировку. Ситуация (X, Y) в биматричной игре с матрицами выигрышей А и В является равновесной, если
![]()
![]() . (5.4)
. (5.4)
![]()
![]() . (5.5)
. (5.5)
Очевидно, что при В = -А биматричная игра превращается в матричную.
В качестве примера рассмотрим биматричную игру «Торг».
Пример. Игра «Торг»
Игрок 1 продает неделимый товар игроку 2. Игрок 1 должен решить, какую назначить цену: высокую или низкую. Для покупателя в принципе приемлемы обе цены. Покупатель не может спорить о цене, он может либо сделать покупку, либо отказаться от нее.
Платежные матрицы игроков имеют вид:
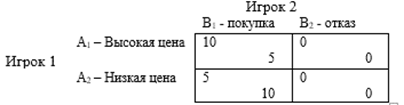
Описание всех возможных ситуаций в этой игре позволяет определить, что ситуация (А1, В1) является оптимальной по Парето и по Нэшу. Ситуация (А2, В2) также является оптимальной по Парето, но не является устойчивой, т. е. оптимальной по Нэшу.
Рассмотрим способ нахождения устойчивых ситуаций для биматричных игр с произвольным количеством чистых стратегий игроков.
| < Предыдущая | Следующая > |
|---|