30. Тесты и задачи 5
(В – Верно, Н – Неверно)
1. Игры называются бесконечными, если у всех игроков множество чистых стратегий бесконечно.
2. Бесконечные антагонистические игры решать труднее, чем конечные.
3. В бесконечной антагонистической игре принципом оптимальности является принцип максимина.
4. Бесконечные антагонистические игры решаются только в чистых стратегиях.
5. Играми на единичном квадрате называются такие бесконечные антагонистические игры, для которых возможные стратегии двух игроков Х и У Î [0,1].
6. Для антагонистических симметричных игр оптимальные стратегии игроков 1 и 2 совпадают.
7. Для антагонистических симметричных игр цена игры V>0.
8. В строго выпуклой игре игрок 2 имеет единственно оптимальную стратегию, которая является чистой.
Найти хотя бы одно решение бесконечной антагонистической игры на единичном квадрате со следующей функцией выигрыша:
1. ![]() ;
;
2. 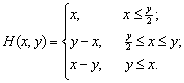
3. 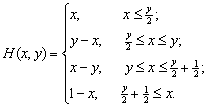
4. ![]()
5. 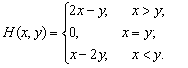
6. ![]()
| < Предыдущая | Следующая > |
|---|